题目内容
19.给出下列关于互不相同的直线m、l、n和平面α、β的四个命题:①若m?α,l∩α=A,点A∉m,则l与m不共面;
②若m、l是异面直线,l∥α,m∥α,且n⊥l,n⊥m,则n⊥α;
③若l∥α,m∥β,α∥β,则l∥m;
④若l?α,m?α,l∩m=A,l∥β,m∥β,则α∥β,
其中为真命题的是( )
| A. | ①③④ | B. | ②③④ | C. | ①②④ | D. | ①②③ |
分析 ①利用异面直线的定义即可判断出正误;
②利用线面垂直的判定定理即可判断出正误;
③由已知可得l与m不一定平行,即可判断出正误;
④利用面面平行的判定定理可得:α∥β,即可判断出正误.
解答 解:①若m?α,l∩α=A,点A∉m,则l与m不共面,正确;
②若m、l是异面直线,l∥α,m∥α,且n⊥l,n⊥m,利用线面垂直的判定定理 即可判断出:n⊥α正确;
③若l∥α,α∥β,α∥β,则l与m不一定平行,不正确;
④若l?α,m?α,l∩m=A,l∥β,m∥β,利用面面平行的判定定理可得:α∥β,正确.
其中为真命题的是①②④.
故选:C.
点评 本题考查了线面平行与垂直的判定定理、异面直线的定义,考查了推理能力,属于中档题.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
9.已知$\frac{tanα+1}{1-tanα}$=1998,则sec2α+tan2α的值为( )
| A. | 1997 | B. | 1998 | C. | 1999 | D. | 2000 |
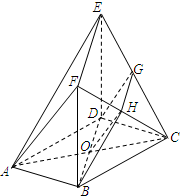 如图,在多面体ABCDEF中,ABCD是边长为2的正方形,DEFB是一平行四边形,且DE⊥平面ABCD,BF=3,G和H分别是CE和CF的中点.
如图,在多面体ABCDEF中,ABCD是边长为2的正方形,DEFB是一平行四边形,且DE⊥平面ABCD,BF=3,G和H分别是CE和CF的中点. 如图,在多面体ABC-A1B1C1中,AB>A1B1,给出如下两个命题:命题甲:AB∥A1B1,BC∥B1C1;命题乙:多面体ABC-A1B1C1是棱台.试问:从命题甲能否推出命题乙?反之,结果如何?
如图,在多面体ABC-A1B1C1中,AB>A1B1,给出如下两个命题:命题甲:AB∥A1B1,BC∥B1C1;命题乙:多面体ABC-A1B1C1是棱台.试问:从命题甲能否推出命题乙?反之,结果如何?