题目内容
【题目】已知动圆
与直线
相切，且与圆
外切.
（1）求动圆圆心轨迹
的方程；
（2）已知过点
的直线
:
与曲线交于
，
两点，是否存在常数
，使得
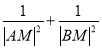恒为定值？
【答案】（1）
；（2）存在
【解析】
(1)根据两点间距离公式及相切条件,即可求得动圆圆心的轨迹方程.
(2)将直线方程与抛物线方程联立,消
后可得关于
的一元二次方程,表示成韦达定理形式.由两点间距离公式,表示出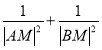
,代入
韦达定理形式,即可得
的表达式.并用换元法,求得
的值即可.
(1)圆
化为标准方程为
则圆心为
,半径为
设动圆
圆心坐标为
,由动圆与直线
相切,且与圆
外切
得
则
两边平方整理得
所以动圆圆心轨迹
的方程为
(2)由题意可将直线
的方程为
与抛物线
联立
消去得
则
,
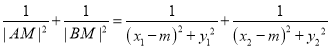
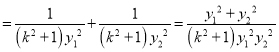
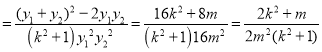
上式对任意
恒为定值,设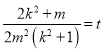
,
整理得
由
,解得
此时
∴存在定点,满足题意
名校课堂系列答案
【题目】“绿水青山就是金山银山”的生态文明发展理念已经深入人心,这将推动新能源汽车产业的迅速发展，下表是近几年我国某地区新能源乘用车的年销售量与年份的统计表：
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
销量（万台） | 8 | 10 | 13 | 25 | 24 |
某机构调查了该地区30位购车车主的性别与购车种类情况，得到的部分数据如下表所示：
购置传统燃油车 | 购置新能源车 | 总计 | |
男性车主 | 6 | 24 | |
女性车主 | 2 | ||
总计 | 30 |
（1）求新能源乘用车的销量
关于年份
的线性相关系数
，并判断与是否线性相关；
（2）请将上述
列联表补充完整，并判断是否有
的把握认为购车车主是否购置新能源乘用车与性别有关；
参考公式：
，
，其中
.
，若
，则可判断与线性相关.
附表：
| 0．10 | 0.05 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【题目】某地区2020年清明节前后3天每天下雨的概率为60%，通过模拟实验的方法来计算该地区这3天中恰好有2天下雨的概率：用随机数
（
，且
）表示是否下雨：当
时表示该地区下雨，当
时，表示该地区不下雨，从随机数表中随机取得20组数如下
332 714 740 945 593 468 491 272 073 445
992 772 951 431 169 332 435 027 898 719
（1）求出
的值，并根据上述数表求出该地区清明节前后3天中恰好有2天下雨的概率；
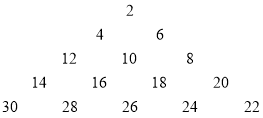
（2）从2011年开始到2019年该地区清明节当天降雨量（单位：
）如下表：（其中降雨量为0表示没有下雨）.
时间 | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 | 2019年 |
年份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
降雨量 | 29 | 28 | 26 | 27 | 25 | 23 | 24 | 22 | 21 |
经研究表明：从2011年开始至2020年， 该地区清明节有降雨的年份的降雨量
与年份
成线性回归，求回归直线
，并计算如果该地区2020年（
）清明节有降雨的话，降雨量为多少？（精确到0.01）
参考公式：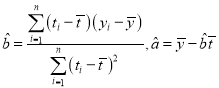
.
参考数据：
，
，
，
.
【题目】某公司为了预测下月产品销售情况，找出了近7个月的产品销售量
（单位：万件）的统计表：
月份代码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售量 |
|
|
|
|
|
|
|
但其中数据污损不清，经查证
，
，
.
（1）请用相关系数说明销售量与月份代码
有很强的线性相关关系；
（2）求关于
的回归方程（系数精确到0.01）；
（3）公司经营期间的广告宣传费
（单位：万元）（
），每件产品的销售价为10元，预测第8个月的毛利润能否突破15万元，请说明理由.（毛利润等于销售金额减去广告宣传费）
参考公式及数据：
，相关系数
，当
时认为两个变量有很强的线性相关关系，回归方程
中斜率和截距的最小二乘估计公式分别为
，
.
【题目】为了节能减排，发展低碳经济，我国政府从2001年起就通过相关政策推动新能源汽车产业发展.下面的图表反映了该产业发展的相关信息:
中国新能源汽车产销情况一览表 | ||||
新能源汽车生产情况 | 新能源汽车销售情况 | |||
产品(万辆) | 比上年同期 | 销量(万辆) | 比上年同期 | |
2018年3月 | 6.8 | 105 | 6.8 | 117.4 |
4月 | 8.1 | 117.7 | 8.2 | 138.4 |
5月 | 9.6 | 85.6 | 10.2 | 125.6 |
6月 | 8.6 | 31.7 | 8.4 | 42.9 |
7月 | 9 | 53.6 | 8.4 | 47.7 |
8月 | 9.9 | 39 | 10.1 | 49.5 |
9月 | 12.7 | 64.4 | 12.1 | 54.8 |
10月 | 14.6 | 58.1 | 13.8 | 51 |
11月 | 17.3 | 36.9 | 16.9 | 37.6 |
1-12月 | 127 | 59.9 | 125.6 | 61.7 |
2019年1月 | 9.1 | 113 | 9.6 | 138 |
2月 | 5.9 | 50.9 | 5.3 | 53.6 |
根据上述图表信息，下列结论错误的是（ ）
A.2017年3月份我国新能源汽车的产量不超过
万辆
B.2017年我国新能源汽车总销量超过
万辆
C.2018年8月份我国新能源汽车的销量高于产量
D.2019年1月份我国插电式混合动力汽车的销量低于
万辆