题目内容
19.已知三棱柱ABC-A1B1C1的底面是正三角形,所有棱长都是6,顶点A1在底面ABC内的射影是△ABC的中心,则四面体A1ABC,B1ABC,C1ABC公共部分的体积等于( )| A. | 6$\sqrt{2}$ | B. | 6$\sqrt{3}$ | C. | 12$\sqrt{2}$ | D. | 12$\sqrt{3}$ |
分析 如图所示,设顶点A1在底面ABC内的射影是△ABC的中心O,连接AO并且延长交BC于点D.可得AO=$\frac{2}{3}$AD.h=A1O=$\sqrt{{A}_{1}{A}^{2}-A{O}^{2}}$.设AB1∩A1B=E,AC1∩A1C=F,
连接CE,BF,CE∩BF=P,则三棱锥P-ABC是四面体A1ABC,B1ABC,C1ABC公共部分.又点P到底面ABC的距离d=$\frac{2}{3}×\frac{1}{2}h$=$\frac{1}{3}h$.S△ABC=$\frac{\sqrt{3}}{4}A{B}^{2}$.VP-ABC=$\frac{1}{3}d{S}_{△ABC}$即可得出.
解答 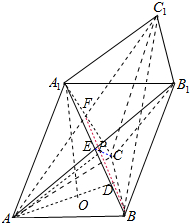
 解:如图所示,
解:如图所示,
设顶点A1在底面ABC内的射影是△ABC的中心O,
连接AO并且延长交BC于点D.
∵AD=$3\sqrt{3}$,∴AO=$\frac{2}{3}$AD=2$\sqrt{3}$.
∴h=A1O=$\sqrt{{A}_{1}{A}^{2}-A{O}^{2}}$=2$\sqrt{6}$.
设AB1∩A1B=E,AC1∩A1C=F,
连接CE,BF,CE∩BF=P,
则三棱锥P-ABC是四面体A1ABC,B1ABC,C1ABC公共部分.
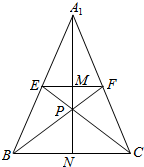
(∵EF是△A1BC的中位线,∴$\frac{PN}{PM}$=$\frac{2}{1}$,∴PN=$\frac{2}{3}MN$=$\frac{2}{3}×\frac{1}{2}{A}_{1}N$=$\frac{1}{3}{A}_{1}N$)
又点P到底面ABC的距离d=$\frac{2}{3}×\frac{1}{2}h$=$\frac{1}{3}h$=$\frac{2}{3}\sqrt{6}$.
S△ABC=$\frac{\sqrt{3}}{4}A{B}^{2}$=$9\sqrt{3}$.
∴VP-ABC=$\frac{1}{3}d{S}_{△ABC}$
=$\frac{1}{3}×\frac{2}{3}\sqrt{6}$×$9\sqrt{3}$
=2$\sqrt{6}$.
故选:A.
点评 本题考查了线面面面垂直的判定与性质定理、三棱锥的体积计算公式、三角形中位线定理、平行线的性质,考查了空间想象能力、推理能力与计算能力,属于中档题.

| A. | 相切 | B. | 相交且直线过圆心 | ||
| C. | 相交且直线不过圆心 | D. | 相离 |
| A. | 2 | B. | $\sqrt{2}$ | C. | 2($\sqrt{3}$+1) | D. | 2($\sqrt{3}$-1) |
| A. | $\frac{1}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
| A. | (0,2] | B. | [$\frac{1}{2}$,2] | C. | [2,+∞) | D. | (0,$\frac{1}{2}$]∪[2,+∞) |