题目内容
9.在极坐标系中,直线l:θ=$\frac{π}{4}$(ρ∈R)和圆C:ρ=1的位置关系是( )| A. | 相切 | B. | 相交且直线过圆心 | ||
| C. | 相交且直线不过圆心 | D. | 相离 |
分析 直线l:θ=$\frac{π}{4}$(ρ∈R)和圆C:ρ=1分别化为直角坐标方程,即可判断出.
解答 解:直线l:θ=$\frac{π}{4}$(ρ∈R)和圆C:ρ=1分别化为直角坐标方程:
直线l的方程:y=x;圆的方程为x2+y2=1.
∴相交且直线过圆心.
故选:B.
点评 本题考查了极坐标方程化为直角坐标方程的方法、直线与圆的位置关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
19.已知三棱柱ABC-A1B1C1的底面是正三角形,所有棱长都是6,顶点A1在底面ABC内的射影是△ABC的中心,则四面体A1ABC,B1ABC,C1ABC公共部分的体积等于( )
| A. | 6$\sqrt{2}$ | B. | 6$\sqrt{3}$ | C. | 12$\sqrt{2}$ | D. | 12$\sqrt{3}$ |
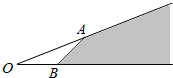 如图所示,两射线OA与OB交于O,则下列选项中哪些向量的终点落在阴影区域内(不含边界)
如图所示,两射线OA与OB交于O,则下列选项中哪些向量的终点落在阴影区域内(不含边界)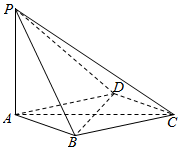 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.