题目内容
8.在各项均为正的数列{an}中,a1=$\frac{1}{2}$,(4n-2)an+1=(2n+1)an,猜想{an}的通项公式并用数学归纳法证明猜想.分析 根据a1=$\frac{1}{2}$,且,(4n-2)an+1=(2n+1)an,利用递推公式,求出a2,a3,a4.总结出规律求出an,然后利用归纳法进行证明,检验n=1时等式成立,假设n=k时命题成立,证明当n=k+1时命题也成立.
解答 解:a1=$\frac{1}{2}$,(4n-2)an+1=(2n+1)an,
∴an+1=$\frac{2n+1}{4n-2}$an,
∴a2=a1•$\frac{3}{2}$=$\frac{3}{4}$,a3=a2•$\frac{3}{4}$=$\frac{5}{8}$,a4=a3•$\frac{5}{8}$=$\frac{7}{16}$,
于是可以猜想an=$\frac{2n-1}{{2}^{n}}$,
证明如下:①当n=1时,a1=$\frac{1}{2}$,猜想成立,
②假设n=k时猜想成立,即ak=$\frac{2k-1}{{2}^{k}}$,
那么当n=k+1时,ak+1=$\frac{2k+1}{4k-2}$•ak=$\frac{2k+1}{2(2k-1)}$•$\frac{2k-1}{{2}^{k}}$=$\frac{2k+1}{{2}^{k+1}}$.
即n=k+1时等式也成立,
由①②可知an=$\frac{2n-1}{{2}^{n}}$,n∈N+.
点评 本题考查归纳推理的应用,着重考查数学归纳法,考查运算推理能力,属于中档题.

练习册系列答案
相关题目
3.已知z=$\frac{2-{i}^{3}}{1-i}$,i是虚数单位,则复数在复平面上对应点落在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
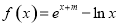 .
. 是函数
是函数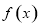 的极值点,求
的极值点,求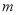 并讨论
并讨论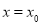 是函数
是函数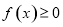 恒成立,求
恒成立,求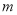 的取值范围(其中常数
的取值范围(其中常数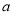 满足
满足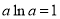 ).
). ,则
,则 ( )
( ) B.
B. C.
C. D.
D.