题目内容
12.已知数列{an}满足:a1+a2+a3+…+an=2n2-15n(n∈N*).(1)求证:数列{an}是等差数列;
(2)求数列{|an|}的前n项和Tn.
分析 (1)由数列的前n项和结合an=Sn-Sn-1(n≥2)求出数列的通项公式,再由等差数列的定义证明;
(2)由(1)可知等差数列为递增数列,求得数列前4项小于0,后面的项大于0,然后分类求得数列{|an|}的前n项和Tn.
解答 (1)证明:由Sn=a1+a2+a3+…+an=2n2-15n,
得a1=-13,
当n≥2时,${a}_{n}={S}_{n}-{S}_{n-1}=2{n}^{2}-15n-[2(n-1)^{2}-15(n-1)]$=4n-17.
当n=1时上式成立.
∴an=4n-17.
∴an+1-an=4(n+1)-17-4n+17=4为常数.
∴数列{an}是等差数列;
(2)解:由(1)知,数列{an}的前n项和${S}_{n}=2{n}^{2}-15n$.
再由an=4n-17≤0,得$n≤\frac{17}{4}$,
∴数列{an}的前4项为负值,第4项以后的项为正值.
则当n≤4时,Tn=-${S}_{n}=15n-2{n}^{2}$;
当n>4时,Tn=-2S4+Sn=2n2-15n+56.
∴${T}_{n}=\left\{\begin{array}{l}{15n-2{n}^{2},n≤4}\\{2{n}^{2}-15n+56,n>4}\end{array}\right.$.
点评 本题考查等差关系的确定,考查了等差数列的前n项和,合理转化是解答该题的关键,是中档题.

练习册系列答案
相关题目
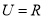 ,集合
,集合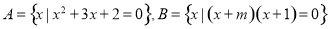 ,若
,若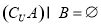 ,求
,求 的值.
的值.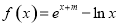 .
. 是函数
是函数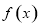 的极值点,求
的极值点,求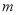 并讨论
并讨论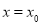 是函数
是函数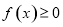 恒成立,求
恒成立,求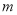 的取值范围(其中常数
的取值范围(其中常数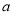 满足
满足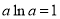 ).
).