题目内容
15.容器A中有m升水,将容器A中的水缓慢注入容器B中,t分钟后容器A中剩余水量y(单位:升)符合函数关系式y=m•3-at(a为正常数).假设经过5分钟后,容器A中的水量和容器B中的水量相等,再经过n分钟,容器A中的水只剩$\frac{m}{8}$,求n的值.分析 由经过5分钟,容器A,B中的水量相等便可得到$\frac{1}{2}m=m•{3}^{-5a}$,从而可以得出a=$\frac{1}{5}lo{g}_{3}2$,这样便可得到$\frac{m}{8}=m•{3}^{-\frac{1}{5}lo{g}_{3}2•(5+n)}$,这样通过两边取对数,便可得出n的值.
解答 解:根据题意:$\frac{1}{2}m=m•{3}^{-5a}$;
∴$a=\frac{1}{5}lo{g}_{3}2$;
∴$\frac{m}{8}=m•{3}^{-\frac{1}{5}lo{g}_{3}2•(5+n)}$;
∴${2}^{-3}={3}^{-\frac{1}{5}lo{g}_{3}2•(5+n)}$;
∴$-3lo{g}_{3}2=-\frac{1}{5}lo{g}_{3}2•(5+n)$;
∴n=10.
点评 考查指数式和对数式互化,以及对数的运算性质,要弄清t,y这两个变量分别表示什么.

练习册系列答案
相关题目
6.如图,在三棱锥V-ABC,VA=VC,VB⊥AC,则AB与BC的大小关系是( )
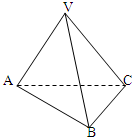

| A. | AB>BC | B. | AB=BC | C. | AB<BC | D. | 无法确定 |
4.下列命题中是真命题的是( )
| A. | 函数y=sin2x的最小正周期是2π | B. | 等差数列一定是单调数列 | ||
| C. | 直线y=ax+a过定点(-1,0) | D. | 在△ABC中,若sinB>0,则B为锐角 |