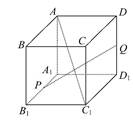
题目内容
设 ,b,c是空间三条不同的直线,
,b,c是空间三条不同的直线, ,
, 是空间两个不同的平面,则下列命题不成立的是( )
是空间两个不同的平面,则下列命题不成立的是( )
A.当 时,若 时,若 ⊥ ⊥ ,则 ,则 ∥ ∥ |
B.当 ,且 ,且 是 是 在 在 内的射影时,若b⊥c,则 内的射影时,若b⊥c,则 ⊥b ⊥b |
C.当 时,若b⊥ 时,若b⊥ ,则 ,则 |
D.当 时,若c∥ 时,若c∥ ,则b∥c ,则b∥c |
D
解析试题分析:A、其逆命题是:当c⊥α时,或α∥β,则c⊥β,由面面平行的性质定理知正确.
B、其逆命题是:当b?α,若α⊥β,则b⊥β,也可能平行,相交.不正确.
C、其逆命题是当b?α,且c是a在α内的射影时,若a⊥b,则b⊥c,由三垂线定理知正确.
D、其逆命题是当b?α,且c?α时,若b∥c,则c∥α,由线面平行的判定定理知正确.故选B.
考点:平面与平面之间的位置关系;四种命题;空间中直线与直线之间的位置关系.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案
相关题目
两直线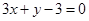 与
与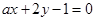 垂直,则
垂直,则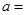 ( )
( )
A.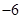 | B.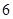 | C.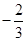 | D.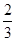 |
已知三棱柱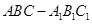 的侧棱
的侧棱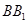 在下底面的射影
在下底面的射影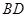 与
与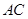 平行,若
平行,若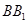 与底面所成角为
与底面所成角为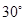 ,且
,且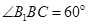 ,则
,则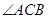 的余弦值为( )
的余弦值为( )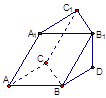
A.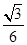 | B.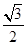 | C.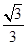 | D.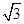 |
设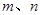 是两条不同的直线,
是两条不同的直线, 是两个不同的平面。下列四个命题正确的是( )
是两个不同的平面。下列四个命题正确的是( )
A.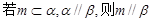 | B.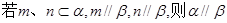 |
C.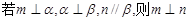 | D.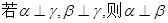 |
设a,b为两条不同的直线,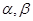 为两个不同的平面,则下列说法正确的是( )
为两个不同的平面,则下列说法正确的是( )
| A.若a∥α,α⊥β,则a∥β | B.若a∥b,a⊥β,则b⊥β |
| C.若a∥α,b∥α,则a∥b | D.若a⊥b,a∥α,则b⊥α |
类比平面内 “垂直于同一条直线的两条直线互相平行”的性质,可推出空间下列结论:
①垂直于同一条直线的两条直线互相平行 ②垂直于同一个平面的两条直线互相平行
③垂直于同一条直线的两个平面互相平行 ④垂直于同一个平面的两个平面互相平行
则正确的结论是 ( )
| A.①② | B.②③ | C.③④ | D.①④ |
给岀四个命题:
(1)若一个角的两边分别平行于另一个角的两边,则这两个角相等;
(2)a,b为两个不同平面,直线aÌa,直线bÌa,且a∥b,b∥b,则a∥b;
(3)a,b为两个不同平面,直线m⊥a,m⊥b,则a∥b;
(4)a,b为两个不同平面,直线m∥a,m∥b,则a∥b .
其中正确的是( )
| A.(1) | B.(2) | C.(3) | D.(4) |
已知m,n为异面直线,m⊥平面α,n⊥平面β.直线l满足l⊥m,l⊥n,l?α,l?β,则( )
| A.α∥β且l∥α |
| B.α⊥β且l⊥β |
| C.α与β相交,且交线垂直于l |
| D.α与β相交,且交线平行于l |