题目内容
在等差数列{an}中,若S9=18,an-4=30,Sn=240.则n等于( )A.9
B.15
C.9或15
D.24
【答案】分析:由题意可得a5,进而可得a1+an=a5+an-4=32,代入已知式子可得n
解答:解:由等差数列的性质可得S9=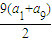 =
=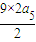 18,
18,
解得a5=2,故a1+an=a5+an-4=32,
故可得Sn=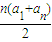 =16n=240,解得n=15
=16n=240,解得n=15
故选B
点评:本题考查等差数列的性质和求和公式,属基础题.
解答:解:由等差数列的性质可得S9=
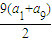 =
=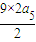 18,
18,解得a5=2,故a1+an=a5+an-4=32,
故可得Sn=
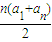 =16n=240,解得n=15
=16n=240,解得n=15故选B
点评:本题考查等差数列的性质和求和公式,属基础题.

练习册系列答案
相关题目