题目内容
8.已知等比数列{an}的前n项和Sn=t•2n-1+1,则实数t的值为( )| A. | -2 | B. | -1 | C. | 2 | D. | 0.5 |
分析 当n≥2,an=Sn-Sn-1=t•2n-2,再由 a1=S1=t+1,可得 t•$\frac{1}{2}$=t+1,由此解得t的值.
解答 解:∵等比数列{an}的前n项和Sn=t•2n-1+1,故当n≥2,an=Sn-Sn-1=t•2n-1+1-t•2n-2-1=t•2n-2.
再由 a1=S1=t+1,可得 t•$\frac{1}{2}$=t+1,解得t=-2,
故选A.
点评 本题主要考查了利用递推公式求,n≥2,an=Sn-Sn-1,当n=1时,a1=S1求解数列的通项公式及等比数列的定义的应用,属于中档题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
18.在各项均为正数的等比数列{an}中,a2,$\frac{1}{2}$a3,a1成等差数列,则公比q的值为( )
| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\frac{\sqrt{5}+1}{2}$ | C. | $\frac{1-\sqrt{5}}{2}$ | D. | $\frac{\sqrt{5}-1}{2}$或$\frac{\sqrt{5}+1}{2}$ |
16.甲乙两人进行射击比赛,各射击5次,成绩(环数)如下表:
(1)分别求出甲、乙射击成绩的平均数及方差,并由此分析两人的射击水平;
(2)若分别对甲、乙两人各取一次成绩,求两人成绩之差不超过2环的概率.
环数 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
| 甲 | 4 | 5 | 7 | 9 | 10 |
| 乙 | 5 | 6 | 7 | 8 | 9 |
(2)若分别对甲、乙两人各取一次成绩,求两人成绩之差不超过2环的概率.
18.设数列{an}是各项为正的单调递减的等比数列,a1+a2+a3=3,则首项a1的取值范围是( )
| A. | (0,3) | B. | (0,1) | C. | (3,9) | D. | (1,3) |
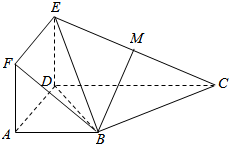 如图,已知多面体ABCDFEF中,平面ADEF⊥平面ABCD,若四边形ADEF为矩形,AB∥CD,$AB=\frac{1}{2}CD$,BC⊥BD,M为EC中点.
如图,已知多面体ABCDFEF中,平面ADEF⊥平面ABCD,若四边形ADEF为矩形,AB∥CD,$AB=\frac{1}{2}CD$,BC⊥BD,M为EC中点.