题目内容
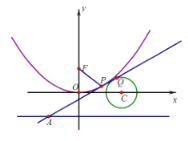
【题目】设抛物线![]() ,
,![]() 满足
满足![]() ,过点
,过点![]() 作抛物线
作抛物线![]() 的切线,切点分别为
的切线,切点分别为![]() .
.
(1)求证:直线![]() 与抛物线
与抛物线![]() 相切;
相切;
(2)若点![]() 坐标为
坐标为![]() ,点
,点![]() 在抛物线
在抛物线![]() 的准线上,求点
的准线上,求点![]() 的坐标;
的坐标;
(3)设点![]() 在直线
在直线![]() 上运动,直线
上运动,直线![]() 是否恒过定点?若恒过定点,求出定点坐标;若不存在,请说明理由;
是否恒过定点?若恒过定点,求出定点坐标;若不存在,请说明理由;
【答案】(1)证明见详解;(2)![]() (3)是,
(3)是,![]()
【解析】
(1)联立直线方程与抛物线方程,由![]() ,即可证明;
,即可证明;
(2)根据点![]() 在抛物线上解得
在抛物线上解得![]() ,进而写出
,进而写出![]() 点坐标,再根据点
点坐标,再根据点![]() 既在直线
既在直线![]() 上,又在抛物线上,联立方程组即可求得
上,又在抛物线上,联立方程组即可求得![]() 的坐标;
的坐标;
(3)写出直线![]() 的方程,根据过点
的方程,根据过点![]() 和过点
和过点![]() 的直线交于点
的直线交于点![]() 得到的结论,整理化简直线方程,即可求得
得到的结论,整理化简直线方程,即可求得![]() 恒过的定点.
恒过的定点.
(1)联立直线![]() 与抛物线方程
与抛物线方程![]() ,消去
,消去![]()
可得![]()
故![]() ,因为点
,因为点![]() 在抛物线上,
在抛物线上,
故![]()
则直线![]() 与抛物线
与抛物线![]() 只有一个交点
只有一个交点
又因为![]() ,故该直线不与
,故该直线不与![]() 轴平行,
轴平行,
即证直线![]() 与抛物线相切.
与抛物线相切.
(2)因为点![]() 在抛物线
在抛物线![]() 上,故可得
上,故可得![]() ,解得
,解得![]()
由(1)可知过点![]() 的切线方程为
的切线方程为![]() ,即
,即![]()
又抛物线的准线方程为![]() ,故令
,故令![]() ,解得
,解得![]() ,
,
即点![]() 的坐标为
的坐标为![]() .
.
因为过点![]() 的切线方程为
的切线方程为![]() ,其过点
,其过点![]()
故可得![]() ,又因为点
,又因为点![]() 满足抛物线方程,
满足抛物线方程,
故可得![]() ,联立方程组可得
,联立方程组可得![]()
解得![]() (舍去,与
(舍去,与![]() 点重合),
点重合),![]() ,
,
故点![]() 的坐标为
的坐标为![]() .
.
(3)由(1)得过![]() 点的切线方程为
点的切线方程为![]()
令![]() ,可解得
,可解得![]()
过![]() 点的切线方程为
点的切线方程为![]()
令![]() ,可解的
,可解的![]()
因为两直线交于点![]() ,故可得
,故可得![]()
整理得![]() ①
①
当过![]() 两点的直线斜率存在,则设其方程为:
两点的直线斜率存在,则设其方程为:![]()
整理得![]() ,将①代入可得
,将①代入可得
故直线方程为![]()
故该直线恒过定点![]() ;
;
当过![]() 两点的直线斜率不存在时,
两点的直线斜率不存在时,
![]() ,代入①可得
,代入①可得![]()
过此时直线![]() ,也经过点
,也经过点![]()
综上所述,直线恒过定点![]() ,即证.
,即证.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案【题目】足球是世界普及率最高的运动,我国大力发展校园足球.为了解本地区足球特色学校的发展状况,社会调查小组得到如下统计数据:
年份x | 2014 | 2015 | 2016 | 2017 | 2018 |
足球特色学校y(百个) | 0.30 | 0.60 | 1.00 | 1.40 | 1.70 |
(1)根据上表数据,计算y与x的相关系数r,并说明y与x的线性相关性强弱.
(已知:![]() ,则认为y与x线性相关性很强;
,则认为y与x线性相关性很强;![]() ,则认为y与x线性相关性一般;
,则认为y与x线性相关性一般;![]() ,则认为y与x线性相关性较):
,则认为y与x线性相关性较):
(2)求y关于x的线性回归方程,并预测A地区2020年足球特色学校的个数(精确到个).
参考公式和数据: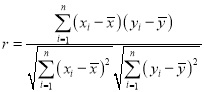 ,
,
![]()
![]()
![]() ,
,
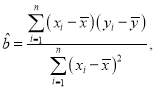
![]() .
.