题目内容
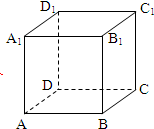 如图在正方体ABCD-A1B1C1D1中,边长为a,E为棱AB的中点.求:
如图在正方体ABCD-A1B1C1D1中,边长为a,E为棱AB的中点.求:(1)C1E与平面ABCD所成的角;(结果用反三角表示)
(2)点B1到平面ABC1D1的距离.
分析:(1)先根据C1C⊥平面ABCD得到EC为EC1在平面ABCD内的射影;进而得到∠C1EC为C1E与平面ABCD所成的角;然后在三角形C1EC中求∠C1EC即可.
(2)过B1作B1H⊥BC1交BC1于点H,先根据条件得到AB⊥B1H;可得B1H⊥平面ABC1D1,然后在等腰直角三角形BB1C1中求出B1H即可.
(2)过B1作B1H⊥BC1交BC1于点H,先根据条件得到AB⊥B1H;可得B1H⊥平面ABC1D1,然后在等腰直角三角形BB1C1中求出B1H即可.
解答:解:(1)连接EC
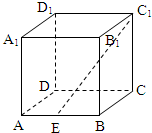
∵C1C⊥平面ABCD---------------------------------(1分)
∴EC为EC1在平面ABCD内的射影--------------------(1分)
∴∠C1EC为C1E与平面ABCD所成的角----------------(2分)
∵C1C=a,EC=
a
∴tan∠C1EC=
=
------------------(2分)
∴C1E与平面ABCD所成的角为arctan
----------------(1分)
(2)连接BC1,AD1,过B1作B1H⊥BC1交BC1于点H
∵AB⊥平面BCC1B1
B1H?平面BCC1B1
∴AB⊥B1H----------------------------------(3分)
又AB∩BC1=B
∴B1H⊥平面ABC1D1-------------------------------(1分)
∴B1H为点B1到平面ABC1D1的距离------------------(1分)
在等腰直角三角形BB1C1中 B1H=
a---------(1分)
∴点B1到平面ABC1D1的距离为
a--------------(1分)

∵C1C⊥平面ABCD---------------------------------(1分)
∴EC为EC1在平面ABCD内的射影--------------------(1分)
∴∠C1EC为C1E与平面ABCD所成的角----------------(2分)
∵C1C=a,EC=
| ||
| 2 |
∴tan∠C1EC=
| a | ||||
|
2
| ||
| 5 |
∴C1E与平面ABCD所成的角为arctan
2
| ||
| 5 |
(2)连接BC1,AD1,过B1作B1H⊥BC1交BC1于点H
∵AB⊥平面BCC1B1
B1H?平面BCC1B1
∴AB⊥B1H----------------------------------(3分)
又AB∩BC1=B
∴B1H⊥平面ABC1D1-------------------------------(1分)
∴B1H为点B1到平面ABC1D1的距离------------------(1分)
在等腰直角三角形BB1C1中 B1H=
| ||
| 2 |
∴点B1到平面ABC1D1的距离为
| ||
| 2 |
点评:本题主要考查直线和平面所成的角以及点到面的距离计算,是对立体几何知识的考查,考查计算能力以及分析问题的能力.

练习册系列答案
相关题目
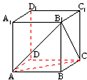 如图在正方体ABCD-A1B1C1D1中,与平面AB1C平行的直线是( )
如图在正方体ABCD-A1B1C1D1中,与平面AB1C平行的直线是( )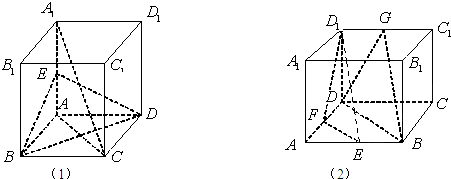
 如图在正方体ABCD-A 1B1C1D1中,O是底面ABCD的中心,B1H⊥D1O,H为垂足,则B1H与平面AD1C的位置关系是( )
如图在正方体ABCD-A 1B1C1D1中,O是底面ABCD的中心,B1H⊥D1O,H为垂足,则B1H与平面AD1C的位置关系是( )