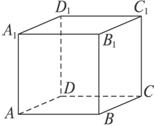
题目内容
（1）如图在正方体ABCD-A1B1C1D1中，E是AA1的中点，求证：A1C∥平面BDE；
（2）如图，在正方体ABCD-A1B1C1D1中，E、F、G分别是AB、AD、C1D1的中点，求证：平面D1EF∥平面BDG．
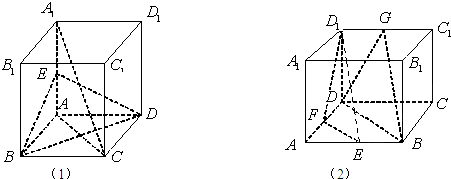
（2）如图，在正方体ABCD-A1B1C1D1中，E、F、G分别是AB、AD、C1D1的中点，求证：平面D1EF∥平面BDG．
分析：（1）连接EO，证EO∥A1C即可；
（2）由面面平行的判定定理，证EF∥BD，D1E∥GB，即可证两个平面平行．
（2）由面面平行的判定定理，证EF∥BD，D1E∥GB，即可证两个平面平行．
解答：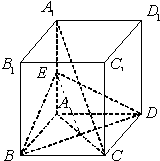
证明：（1）设AC∩BD=O
∵E、O分别是AA1、AC的中点，∴A1C∥EO
∵OE?平面BDE，A1C?平面BDE
∴A1C∥平面BDE
（2）∵E、F分别是AA1、AD的中点，∴EF∥BD
又EF?平面BDG，BD?平面BDG
∴EF∥平面BDG
∵D1G∥EB且D1G=EB
∴四边形D1GBE为平行四边形，D1E∥GB
又D1E?平面BDE，GB?平面BDG
∴D1E∥平面BDG
∵EF∩D1E=E
∴平面D1EF∥平面BDG
证明：（1）设AC∩BD=O∵E、O分别是AA1、AC的中点，∴A1C∥EO
∵OE?平面BDE，A1C?平面BDE
∴A1C∥平面BDE
（2）∵E、F分别是AA1、AD的中点，∴EF∥BD
又EF?平面BDG，BD?平面BDG
∴EF∥平面BDG
∵D1G∥EB且D1G=EB
∴四边形D1GBE为平行四边形，D1E∥GB
又D1E?平面BDE，GB?平面BDG
∴D1E∥平面BDG
∵EF∩D1E=E
∴平面D1EF∥平面BDG
点评：本题主要考查了线面平行、面面平行的判定，属常规题型．
练习册系列答案
发散思维新课堂系列答案
相关题目
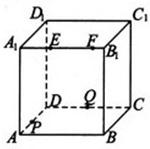如图，正方体ABCD-A1B1C1D1的棱长为2，动点E、F在棱A1B1上，动点P，Q分别在棱AD，CD上，若EF=1，A1E=x，DQ=y，DP=z（x，y，z大于零），则四面体PEFQ的体积（ ）| A、与x，y，z都有关 | B、与x有关，与y，z无关 | C、与y有关，与x，z无关 | D、与z有关，与x，y无关 |
如图在正方体ABCD-A1B1C1D1中，边长为a，E为棱AB的中点．求：
