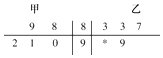题目内容
【题目】集合P={x|a+1≤x≤2a+1}，Q={x|﹣2≤x≤5}
（1）若a=3，求集合（RP）∩Q；
（2）若PQ，求实数a的取值范围．
【答案】
（1）解：将a=3代入得：P={x|4≤x≤7}，可得RP={x|x＜4或x＞7}，
∵Q={x|﹣2≤x≤5}，∴（RP）∩Q={x|﹣2≤x＜4}
（2）解：由PQ，分两种情况考虑：
（ⅰ）当P≠时，根据题意得：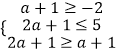 
，解得：0≤a≤2；
（ⅱ）当P=时，可得2a+1＜a+1，解得：a＜0，
综上：实数a的取值范围为（﹣∞，2]
【解析】（1）将a的值代入集合P中的不等式，确定出P，找出P的补集，求出P补集与Q的交集即可；（2）根据P为Q的子集列出关于a的不等式组，求出不等式组的解集即可得到a的范围．
练习册系列答案
相关题目
【题目】一台机器按不同的转速生产出来的某机械零件有一些会有缺点，每小时生产有缺点零件的多少，随机器的运转的速度而变化，具有线性相关关系，下表为抽样试验的结果：
转速x（转/秒） | 8 | 10 | 12 | 14 | 16 |
每小时生产有缺点的零件数y（件） | 5 | 7 | 8 | 9 | 11 |
（1）如果y对x有线性相关关系，求回归方程；
（2）若实际生产中，允许每小时生产的产品中有缺点的零件最多有10个，那么机器的运转速度应控制在设么范围内？
【题目】某化肥厂甲、乙两个车间包装肥料，在自动包装传送带上每隔30分钟抽取一包产品，称其重量，分别记录抽查数据如下：
甲 | 102 | 101 | 99 | 98 | 103 | 98 | 99 |
乙 | 110 | 115 | 90 | 85 | 75 | 115 | 110 |
（1）这种抽样方法是哪一种？
（2）将两组数据用茎叶图表示．
（3）将两组数据进行比较，说明哪个车间产品较稳定．
