题目内容

曲线C1的极坐标方程为：ρ=2sinθ，曲线C2的参数方程为：
y=2+3t
x=1-4t
（t为参数），P在曲线C1上，Q在曲线C2上，则P与Q的最大距离为：（　　）
分析：曲线C1的普通方程为x2+（y-1）2=1，表示以C（0，1）为圆心，半径为1 的圆．曲线C2的普通方程为3x+4y=11．利用直线和圆的位置关系求解．
解答：解：曲线C1的极坐标方程为：ρ=2sinθ，即ρ2=2ρsinθ，化为普通方程为x2+y2=2y，即为x2+（y-1）2=1
表示以C（0，1）为圆心，半径为1 的圆．
曲线C2的参数方程为
y=2+3t   ①
x=1-4t    ②
，①×4+②×3，消去t得普通方程为3x+4y=11．

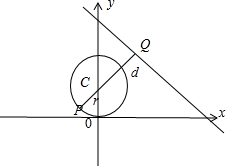
如图，CQ⊥l，垂足为Q，d=
7
5
，当P，C，Q共线时，P与Q的距离最大，此时|PQ|=d+r=1+
7
5
=
12
5
．
故选B
点评：本题考查参数方程、极坐标方程、普通方程的互化，以及应用，数形结合的思想．
练习册系列答案
相关题目
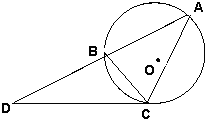（1）圆O是△ABC的外接圆，过点C的圆的切线与AB的延长线交于点D，CD=2
7
，AB=BC=3，求BD以及AC的长．
（2）已知曲线C1的极坐标方程为ρ=6cosθ，曲线C2的极坐标方程为θ=
π
4
，曲线C1，C2相交于A，B两点
（I）把曲线C1，C2的极坐标方程转化为直角坐标方程；
（II）求弦AB的长度．
（3）已知a，b，c都是正数，且a，b，c成等比数列，求证：a2+b2+c2＞（a-b+c）2．
本题设有（1）、（2）、（3）三个选考题，每题7分，请考生任选2题作答，满分14分
（1）选修4-2：矩阵与变换
变换T是将平面上每个点M（x，y）的横坐标乘2，纵坐标乘4，变到点M′（2x，4y）．
（Ⅰ）求变换T的矩阵；
（Ⅱ）圆C：x2+y2=1在变换T的作用下变成了什么图形？
（2）选修4-4：坐标系与参数方程
已知极点与原点重合，极轴与x轴的正半轴重合．若曲线C1的极坐标方程为：5ρ2-3ρ2cos2θ-8=0，直线?的参数方程为：
x=1-
3
t
y=t
（t为参数）．
（Ⅰ）求曲线C1的直角坐标方程；
（Ⅱ）直线?上有一定点P（1，0），曲线C1与?交于M，N两点，求|PM|．|PN|的值．
（3）选修4-5：不等式选讲
已知a，b，c为实数，且a+b+c+2-2m=0，a2+
1
4
b2+
1
9
c2+m-1=0．
（Ⅰ）求证：a2+
1
4
b2+
1
9
c2≥
(a+b+c)2
14
；
（Ⅱ）求实数m的取值范围．
（2012•虹口区三模）（理科）曲线C1的极坐标方程是ρ=4cosθ，直线l的极坐标方程是ρsinθ=2cos
π
6
，则它们的交点的直角坐标是
(1，
3
)，(3，
3
)
(1，
3
)，(3，
3
)
．
选修4-4：坐标系与参数方程
已知曲线C1的极坐标方程为ρ=4sinθ，曲线C2的极坐标方程为θ=
π6
(ρ∈R)，曲线C1，C2相交于点M，N．
（1）将曲线C1，C2的极坐标方程化为直角坐标方程；
（2）求线段MN的长．
在平面直角坐标系xOy中，以坐标原点O为极点x轴的正半轴为极轴建立极坐标系，曲线C1的极坐标方程为：3ρ2=12ρcosθ-10（ρ＞0）．
（1）求曲线C1的普通方程
（2）曲线C2的方程为
x2
16
+
y2
4
=1，设P、Q分别为曲线C1与曲线C2上的任意一点，求|PQ|的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网