��Ŀ����
����Ŀ�������� ![]() ���㣺��
���㣺�� ![]() ����������
���������� ![]() ����
���� ![]() ��
��
�輯�� ![]() ��������
�������� ![]() �е�Ԫ�ص����ֵ��Ϊ
�е�Ԫ�ص����ֵ��Ϊ ![]() �����仰˵��
�����仰˵�� ![]() ��
��
���� ![]() �����㲻��ʽ
�����㲻��ʽ ![]() ������������������ֵ�����dz�����
������������������ֵ�����dz����� ![]() Ϊ����
���� ![]() ��
��
�������У����磬����1,3,5�İ�������Ϊ1,1,2,2,3��
��1�������� ![]() �İ�������Ϊ1,1,1,2,2,2,3����д������
�İ�������Ϊ1,1,1,2,2,2,3����д������ ![]() ��
��
��2���� ![]() ��������
�������� ![]() ��������
�İ������� ![]() ��ǰ100֮�ͣ�
��ǰ100֮�ͣ�
��3�������� ![]() ��ǰ
��ǰ ![]() ���
��� ![]() ������
������ ![]() ����������������
���������������� ![]() ��������
�İ������� ![]() ǰ
ǰ ![]() ���
��� ![]() ��
��
���𰸡�
��1���⣺1,4,7
��2���⣺�� ![]() ����
���� ![]()
�� �� ![]() ʱ��
ʱ�� ![]()
�� ![]() ʱ��
ʱ�� ![]()
�� ![]() ʱ��
ʱ�� ![]()
�� ![]() ʱ��
ʱ�� ![]()
�� ![]() ʱ��
ʱ�� ![]()
�� ![]()
��3���⣺�� ![]() ��
�� ![]()
�� ![]() ʱ��
ʱ�� ![]()
�� ![]()
�� ![]() �ã�
�ã� ![]()
��ʹ�� ![]() ������
������ ![]() �����ֵΪ
�����ֵΪ ![]() ��
��
�� ![]()
�� ![]() ʱ��
ʱ�� ![]()
�� ![]() ʱ��
ʱ�� ![]()
�� ![]() ʱ��
ʱ�� ![]()
�� 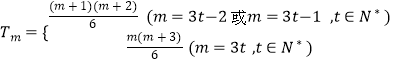
���������Ȳ�����ͨ�ʽ��an=a1+(n-1)d���Ȳ����е�ǰn���ʽ��![]() ���ȱ�����ͨ�ʽ��an = a1qn-1 ��a1�� q�� 0 �����ȱ����е�ǰn���ʽ����q=1ʱ��Sn = na1 ����q�� 1ʱ��
���ȱ�����ͨ�ʽ��an = a1qn-1 ��a1�� q�� 0 �����ȱ����е�ǰn���ʽ����q=1ʱ��Sn = na1 ����q�� 1ʱ��![]() ��
��

 ÿ�α���ϵ�д�
ÿ�α���ϵ�д� ��ѧ����ϵ�д�
��ѧ����ϵ�д�����Ŀ��������ij��ɽ������Ϊ�˽�ɽ��y�����ף�������x���棩֮��Ĺ�ϵ�����ͳ����4��ɽ������Ӧ�����£��������˶��ձ����ɱ������ݣ��õ����Իع鷽��Ϊy=��2x+a���ɴ˹���ɽ��Ϊ72�����ף���������Ϊ�� ��
����x���棩 | 18 | 13 | 10 | ��1 |
ɽ��y�����ף� | 24 | 34 | 38 | 64 |
A.��10
B.��8
C.��6
D.��4
����Ŀ������������פ���У���ɫ��������ʱ�У�ij����ͳ��������ʾ��2016����й��������û�����ȼ��ֲ���ͼ1��ʾ��һ��������ʹ�õ�����Ƶ�ʷֲ�����ͼ��ͼ2��ʾ���������������û����������Ϊ�������ˡ���20�ꡫ39�꣩�͡��������ˡ���19�꼰���»���40�꼰���ϣ����࣬��һ����ʹ�õĴ���Ϊ6�λ�6�����ϵij�Ϊ������ʹ�õ����û�����ʹ�ô���Ϊ5�λ���5�εij�Ϊ������ʹ�õ����û�������֪�ڡ�����ʹ�õ����û������� ![]() �ǡ������ˡ���
�ǡ������ˡ��� 
�����ֶԸ���������С�����ʹ�ù��������������ϵ���ĵ��飬������������ķ�������ȡһ������Ϊ200���������������ͼ���е����ݣ���ȫ����2��2���������������������Ķ����Լ��飬�ж����ж����տ�����Ϊ����ʹ�ù��������������йأ�
ʹ�ù����������������������
������ | �������� | �ϼ� | |
����ʹ�ù��������û� | 120 | ||
����ʹ�ù��������û� | 80 | ||
�ϼ� | 160 | 40 | 200 |
����Ƶ����Ϊ���ʣ����Ӹ��������������ȡ3�ˣ������о���ʹ�ù��������ġ��������ˡ�����Ϊ�������X����X�ķֲ�����������
���ο����ݣ�
P��K2��k0�� | 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
����K2= ![]() ��n=a+b+c+d��
��n=a+b+c+d��