题目内容
【题目】已知数列
中， 
，数列
满足
．
（1）求证：数列是等差数列。
（2）试确定数列中的最大项和最小项，并求出相应项的值。
【答案】（1）见解析；（2）最小项为
且
，最大项为
且
.
【解析】
（1）把给出的
变形得anan﹣1=2an﹣1﹣1，然后直接求bn+1﹣bn，把bn+1和bn用an+1和an表示后整理即可得到结论；（2）求出数列{bn}的通项公式，则数列{an}的通项公式可求，然后利用数列的函数特性可求其最大项和最小项．
（1）证明：由
，得：anan﹣1=2an﹣1﹣1，则an+1an=2an﹣1．
又
，
∴bn+1﹣bn=
=
=
=
=1．
∴数列{bn}是等差数列；
（2）解：∵
，
，
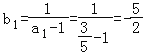又数列{bn}是公差为1的等差数列，
∴
，
则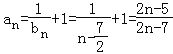
=
，
当n=4时，取最大值3，当n=3时，取最小值﹣1．
故数列{an}中的最大项是a4=3，最小项是a3=﹣1．
练习册系列答案
阅读快车系列答案
相关题目
