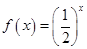题目内容
(本题满分12分)
函数 对任意实数
对任意实数 都有
都有 ,
,
(Ⅰ)分别求 的值;
的值;
(Ⅱ)猜想
 的表达式,并用数学归纳法证明你的结论.
的表达式,并用数学归纳法证明你的结论.
(1)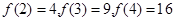 。(2)
。(2)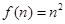 。
。
解析试题分析:(Ⅰ) ,
, --------6分
--------6分
(Ⅱ)猜想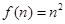 , ---------8分
, ---------8分
下用数学归纳法证明之.
(1)当n=1时,f(1)=1,猜想成立;
(2)假设当n=k时,猜想成立,即 f(k)=k2
则当n=k+1时, f(k+1)=f(k)+f(1)+2k×1=k2+2k+1=(k+1)2
即当n=k+1时猜想成立。
由(1)、(2)可知,对于一切n∈N*猜想均成立。 ---------12分
考点:抽象函数及应用;数学归纳法。
点评:本题目主要考查了利用赋值法求解抽象函数的函数值,及数学归纳法在证明数学命题中的应用。属于中档题。

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 ,设
,设 。
。 图象上任意一点
图象上任意一点 为切点的切线的斜率
为切点的切线的斜率 恒成立,求实数
恒成立,求实数 的最小值。
的最小值。 ,使得函数
,使得函数 的图象与
的图象与 的图象恰好有四个不同的交点?若存在,求出
的图象恰好有四个不同的交点?若存在,求出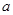 ∈R,函数
∈R,函数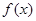 =
=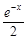 (
(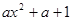 ),其中e是自然对数的底数.
),其中e是自然对数的底数.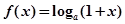 ,
,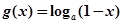 ,其中
,其中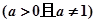 ,设
,设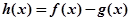 .
.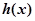 的奇偶性,并说明理由;
的奇偶性,并说明理由;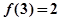 ,求使
,求使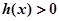 成立的x的集合。
成立的x的集合。
 有三个不同的实根.
有三个不同的实根. =
=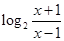 .
.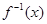 ,并求使得函数
,并求使得函数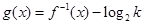 有零点的实数
有零点的实数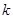 的取值范围.
的取值范围. 对任意的实数
对任意的实数 ,
, ,均有
,均有 ,则称函数
,则称函数 上的“平缓函数”.
上的“平缓函数”.  和
和 是不是实数集R上的“平缓函数”,并说明理由;
是不是实数集R上的“平缓函数”,并说明理由; 对所有的正整数
对所有的正整数 都有
都有  ,设
,设 ,
,  .
.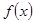 是
是 上的增函数,设
上的增函数,设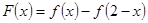 。
。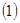 用定义证明:
用定义证明: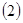 证明:如果
证明:如果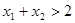 ,则
,则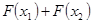 >0,(6分)
>0,(6分) 定义在R上的偶函数,当
定义在R上的偶函数,当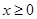 时,
时,