题目内容
(本小题满分12分)
设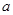 ∈R,函数
∈R,函数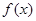 =
=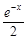 (
(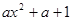 ),其中e是自然对数的底数.
),其中e是自然对数的底数.
(1)判断f (x)在R上的单调性;
(2)当– 1 <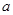 < 0时,求f (x)在[1,2]上的最小值.
< 0时,求f (x)在[1,2]上的最小值.
选做题:请考生从给出的3道题中任选一题做答,并在答题卡上把所选题目的题号用2B铅笔涂黑.注意所做题目的题号必须与所涂的题号一致,在答题卡选答区域指定位置答题.如果多做,则按所做的第一题计分.
(1)在区间(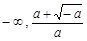 )上, f (x)单调递增;在区间(
)上, f (x)单调递增;在区间(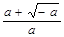 ,
,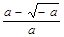 )上, f (x)单调递减;在区间(
)上, f (x)单调递减;在区间(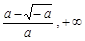 )上, f (x)单调递增.
)上, f (x)单调递增.
(2)f (x)在[1,2]上的最小值为f(2) =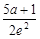
解析试题分析:(1)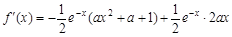 =
=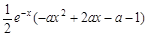 . ……2 分
. ……2 分
因为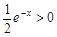 ,以下讨论函数g (x) = –a
,以下讨论函数g (x) = –a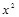 + 2ax – a – 1值的情况.
+ 2ax – a – 1值的情况.
当a = 0时,g (x) =" –1" < 0,即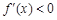 ,所以f (x)在R上是减函数. ……3分
,所以f (x)在R上是减函数. ……3分
当a > 0时,g (x) = 0的判别式Δ= 4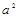 – 4(
– 4(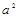 +a) =" –4a" < 0,
+a) =" –4a" < 0,
所以g(x)<0,即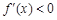 ,所以f(x)在R上是减函数. ……5分
,所以f(x)在R上是减函数. ……5分
当a < 0时,g (x) = 0有两个根,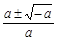 ,并且
,并且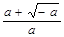 <
<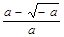 ,
,
所以,在区间(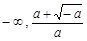 )上,g (x) > 0,即
)上,g (x) > 0,即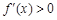 ,f (x)在此区间上 是增函数.
,f (x)在此区间上 是增函数.
在区间(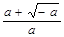 ,
,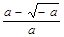 )上,g (x) < 0,即
)上,g (x) < 0,即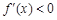 ,f (x)在此区间上是减函数.
,f (x)在此区间上是减函数.
在区间(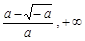 )上,g (x) > 0,即
)上,g (x) > 0,即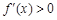 ,f (x)在此区间上是增函数. ……7分
,f (x)在此区间上是增函数. ……7分
综上,当a≥0时,f (x)在R上是减函数;
当a < 0时,f (x)在(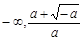 )上单调递增,在(
)上单调递增,在(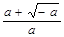 ,
,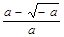 )上单调递减,在(
)上单调递减,在(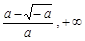 )上单调递增. ……8分
)上单调递增. ……8分
(2)当 – 1 < a < 0时,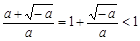 ,
,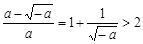 , ……10分
, ……10分
所以,在区间[1,2]上,函数f (x)单调递减, ……11分
所以,函数f (x)在区间[1,2]上的最小值为f (2) =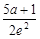 . ……12分
. ……12分
考点:本小题主要考查利用导数考查函数的单调性和最值问题,考查学生分类讨论思想的应用.
点评:在高考解答题中,经常用到分类讨论思想,分类讨论时要准确确定分类标准,分类标准要不重不漏.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 ,其图象在点
,其图象在点 处的切线方程为
处的切线方程为
 的值;
的值; 的单调区间,并求出
的单调区间,并求出 (
( 为实常数)为奇函数,函数
为实常数)为奇函数,函数 .
. 在
在 上的最大值;
上的最大值; 时,
时, 对所有的
对所有的 及
及 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 的表达式,并判断
的表达式,并判断 时,恒有
时,恒有 求m的取值范围。
求m的取值范围。 是定义在R上的偶函数,当
是定义在R上的偶函数,当 时,
时,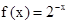 .
.
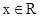 时,
时, 对任意实数
对任意实数 都有
都有 ,
,
 的值;
的值;
 的表达式,并用数学归纳法证明你的结论.
的表达式,并用数学归纳法证明你的结论.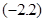 上的奇函数
上的奇函数 ,满足
,满足 ,又当
,又当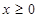 时,
时,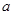 的取值范围。
的取值范围。