题目内容
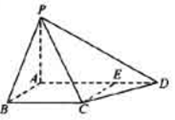
如图,在四棱锥 中,
中, 底面
底面 ,
, ,
, ,
, ,
,
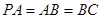 .
.

(1)若E是PC的中点,证明: 平面
平面 ;
;
(2)试在线段PC上确定一点E,使二面角P- AB- E的大小为 ,并说明理由.
,并说明理由.
 中,
中, 底面
底面 ,
, ,
, ,
, ,
,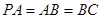 .
.
(1)若E是PC的中点,证明:
 平面
平面 ;
;(2)试在线段PC上确定一点E,使二面角P- AB- E的大小为
 ,并说明理由.
,并说明理由.(1)先证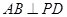 ,再证
,再证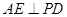 ,利用线面垂直的判定定理即可证明
,利用线面垂直的判定定理即可证明
(2)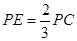
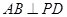 ,再证
,再证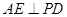 ,利用线面垂直的判定定理即可证明
,利用线面垂直的判定定理即可证明(2)
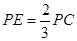
试题分析:(1)证明:
 ,
,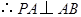 ,
,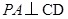 ,
,又
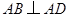 ,
, ,
,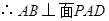 ,
,  , 4 分
, 4 分 ,
,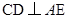 ,
,又
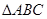 中,
中,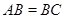 ,
,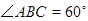 ,
,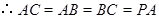 ,
,又
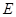 是PC中点,
是PC中点,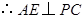
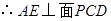
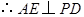
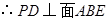 7分
7分(2)过E作
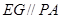 交AC于G,过G作GH⊥AB,垂足为H,则由
交AC于G,过G作GH⊥AB,垂足为H,则由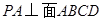 知 ,
知 ,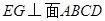 ,
,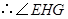 是二面角
是二面角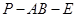 的平面角的余角,即
的平面角的余角,即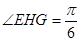 . 10分
. 10分设
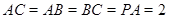 ,
,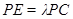 ,则
,则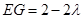 ,
, 12分
12分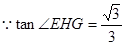 ,
,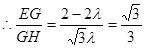 ,
, 14分
14分方法二(向量法)
如图,分别以
 为x,y,z轴建立空间直角坐标系,设
为x,y,z轴建立空间直角坐标系,设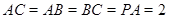
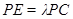 ,则A(0,0,0),B(2,0,0),P(0,0,2),C(1,
,则A(0,0,0),B(2,0,0),P(0,0,2),C(1,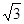 ,0),E(
,0),E(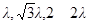 ) 9分
) 9分设平面
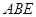 的一个法向量
的一个法向量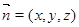 ,则
,则由
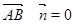 及
及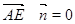 得
得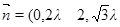 ) 11分
) 11分而平面PAB的一法向量
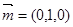 , 12分
, 12分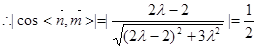 ,解得
,解得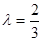 ,即
,即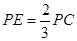 14分
14分点评:解决立体几何问题,可以用判定定理和性质定理进行证明,也可以用空间向量求解,两种方法各有利弊,注意用传统的方法证明或求解时,要紧扣相应的判定定理和性质定理,定理中要求的条件缺一不可,而如果用向量解决问题,要注意各个量尤其是角的取值范围.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
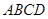 中,
中,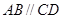 ,
,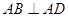 ,且
,且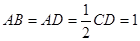 .
.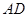 为一边向形外作正方形
为一边向形外作正方形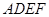 ,然后沿边
,然后沿边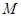 为
为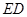 的中点,如图2.
的中点,如图2.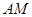 ∥平面
∥平面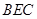 ;
;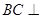 平面
平面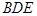 ;
;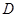 到平面
到平面
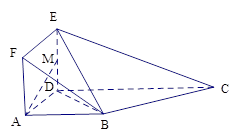
 图
图
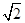 ,∠CDA=45°,求四棱锥P-ABCD的体积
,∠CDA=45°,求四棱锥P-ABCD的体积 ,动点P.Q分别在面α.β内,P到β的距离为
,动点P.Q分别在面α.β内,P到β的距离为 ,Q到α的距离为
,Q到α的距离为 ,则P. Q两点之间距离的最小值为 ;
,则P. Q两点之间距离的最小值为 ; 中,对角线
中,对角线 于
于 ,
, ,
, 为
为 的重心,过点
的重心,过点 分别交
分别交 于
于 且
且 ,沿
,沿 将
将 折起,沿
折起,沿 折起,
折起, 正好重合于
正好重合于 .
. 
 平面
平面 ;
;  与平面
与平面 夹角的大小.
夹角的大小.  边长为
边长为 ,角
,角 ,沿
,沿 将
将 折起,使二面角
折起,使二面角 为
为 ,则折起后
,则折起后 、
、 之间的距离是 .
之间的距离是 .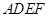 与梯形
与梯形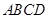 所在的平面互相垂直,
所在的平面互相垂直,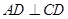 ,
,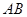 ∥
∥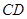 ,
,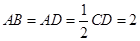 ,点
,点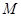 在线段
在线段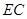 上.
上.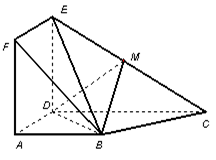
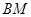 ∥平面
∥平面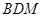 与平面
与平面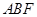 所成锐二面角的余弦值为
所成锐二面角的余弦值为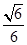 时,求三棱锥
时,求三棱锥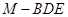 的体积.
的体积.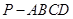 中,
中, 底面
底面 ,
, ,
, ,
, 是
是 的中点.
的中点.
 ;
; 平面
平面 ;
; 和两条不重合的直线m,n,则下列四种说法正确的为( )
和两条不重合的直线m,n,则下列四种说法正确的为( ) α,则m∥α
α,则m∥α