题目内容
已知函数f(x)=sinx+cosx,则函数F(x)=f(x)f′(x)+f2(x)的最大值是
- A.

- B.

- C.

- D.
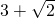
B
分析:先计算f′(x),然后化简F(x)=sin2x+cos2x+1= sin(2x+
sin(2x+ )+1,即可求出F(x)的最大值.
)+1,即可求出F(x)的最大值.
解答:∵f′(x)=cosx-sinx,
∴F(x)=(sinx+cosx)(cosx-sinx)+(sinx+cosx)2
=cos2x-sin2x+2sinxcosx+1
=cos2x+sin2x+1
= sin(2x+
sin(2x+ )+1,
)+1,
∵sin(2x+ )≤1,
)≤1,
∴F(x)的最大值是 +1.
+1.
故选B.
点评:此题考查了三角恒等变换及三角函数的最值,用到了三角函数的倍角公式及平方关系,特别是将式子asinx+bcosx化为 sin(x+φ),对于当φ是特殊角时要求学生熟练掌握.
sin(x+φ),对于当φ是特殊角时要求学生熟练掌握.
分析:先计算f′(x),然后化简F(x)=sin2x+cos2x+1=
 sin(2x+
sin(2x+ )+1,即可求出F(x)的最大值.
)+1,即可求出F(x)的最大值.解答:∵f′(x)=cosx-sinx,
∴F(x)=(sinx+cosx)(cosx-sinx)+(sinx+cosx)2
=cos2x-sin2x+2sinxcosx+1
=cos2x+sin2x+1
=
 sin(2x+
sin(2x+ )+1,
)+1,∵sin(2x+
 )≤1,
)≤1,∴F(x)的最大值是
 +1.
+1.故选B.
点评:此题考查了三角恒等变换及三角函数的最值,用到了三角函数的倍角公式及平方关系,特别是将式子asinx+bcosx化为
 sin(x+φ),对于当φ是特殊角时要求学生熟练掌握.
sin(x+φ),对于当φ是特殊角时要求学生熟练掌握. 
练习册系列答案
相关题目
