题目内容
【题目】如图,在多面体ABCDEF中,底面ABCD为正方形,平面AED⊥平面ABCD,AB= ![]() EA=
EA= ![]() ED,EF∥BD
ED,EF∥BD 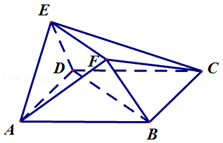
(I)证明:AE⊥CD
(II)在棱ED上是否存在点M,使得直线AM与平面EFBD所成角的正弦值为 ![]() ?若存在,确定点M的位置;若不存在,请说明理由.
?若存在,确定点M的位置;若不存在,请说明理由.
【答案】解:(I)证明:∵四边形ABCD是正方形,∴CD⊥AD, 又平面AED⊥平面ABCD,平面AED∩平面ABCD=AD,CD平面ABCD,
∴CD⊥平面AED,∵AE平面AED,
∴AE⊥CD.
(II)解:取AD的中点O,过O作ON∥AB交BC于N,连接EO,
∵EA=ED,∴OE⊥AD,又平面AED⊥平面ABCD,平面AED∩平面ABCD=AD,OE平面AED,
∴OE⊥平面ABCD,
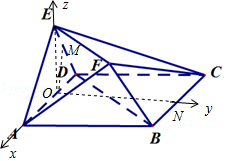
以O为原点建立空间直角坐标系O﹣xyz,如图所示:
设正方形ACD的边长为2, ![]() ,
,
则A(1,0,0),B(1,2,0),D(﹣1,0,0),E(0,0,1),M(﹣λ,0,λ)
∴ ![]() =(﹣λ﹣1,0,λ),
=(﹣λ﹣1,0,λ), ![]() =(1,0,1),
=(1,0,1), ![]() =(2,2,0),
=(2,2,0),
设平面BDEF的法向量为 ![]() =(x,y,z),
=(x,y,z),
则 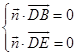 ,即
,即 ![]() ,令x=1得
,令x=1得 ![]() =(1,﹣1,﹣1),
=(1,﹣1,﹣1),
∴cos< ![]() >=
>= 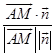 =
= ![]() ,
,
令| ![]() |=
|= ![]() ,方程无解,
,方程无解,
∴棱ED上不存在点M,使得直线AM与平面EFBD所成角的正弦值为 ![]() .
.
【解析】(I)利用面面垂直的性质得出CD⊥平面AED,故而AE⊥CD;(II)取AD的中点O,连接EO,以O为原点建立坐标系,设 ![]() ,求出平面BDEF的法向量
,求出平面BDEF的法向量 ![]() ,令|cos<
,令|cos< ![]() >|=
>|= ![]() ,根据方程的解得出结论.
,根据方程的解得出结论.
【考点精析】本题主要考查了直线与平面垂直的性质和空间角的异面直线所成的角的相关知识点,需要掌握垂直于同一个平面的两条直线平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则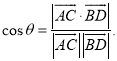 才能正确解答此题.
才能正确解答此题.

 53随堂测系列答案
53随堂测系列答案
