题目内容
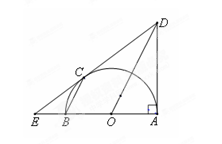
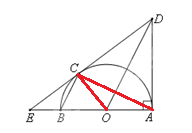
如图,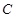 是以
是以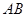 为直径的半圆
为直径的半圆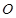 上的一点,过
上的一点,过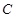 的直线交直线
的直线交直线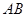 于
于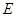 ,交过A点的切线于
,交过A点的切线于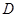 ,
,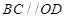 .
.
(Ⅰ)求证: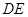 是圆
是圆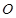 的切线;
的切线;
(Ⅱ)如果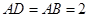 ,求
,求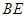 .
.
(Ⅰ)见解析;(Ⅱ) 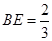 .
.
解析试题分析:(Ⅰ) 连接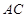 ,
,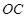 ,根据直径所对的圆心角是直角可知,
,根据直径所对的圆心角是直角可知,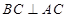 ,结合已知条件“
,结合已知条件“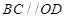 ”得,
”得,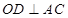 ,所以
,所以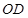 是
是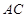 的中垂线,由中垂线的性质可得到,
的中垂线,由中垂线的性质可得到,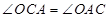 ,
, ,把角
,把角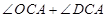 转化为
转化为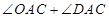 ,即可得到
,即可得到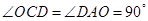 ,则结论可证;(Ⅱ)先根据两个对应角相等得到
,则结论可证;(Ⅱ)先根据两个对应角相等得到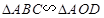 ,由相似三角形对应线段成比例求出线段
,由相似三角形对应线段成比例求出线段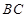 的值,进一步求出
的值,进一步求出 的值,由平行线分线段成比例可得到
的值,由平行线分线段成比例可得到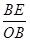 的值,从而解出
的值,从而解出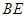 .
.
试题解析:(Ⅰ)连接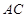 ,
,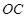 ,
,
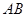 是直径,则
是直径,则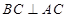 .
.
由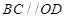 得,
得,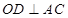 ,
,
则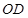 是
是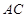 的中垂线,
的中垂线,
所以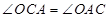 ,
, ,
,
所以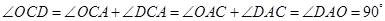 ,
,
则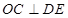 ,即
,即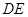 是圆
是圆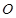 的切线. 5分
的切线. 5分
(Ⅱ)因为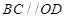 ,
,
所以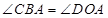 ,
,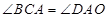 ,
,
则有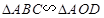 ,
,
所以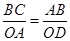 ,那么
,那么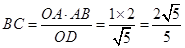 ,
,
所以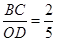 ,
,
所以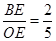 ,
,
所以 ,
,
解得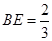 . 10分
. 10分
考点:1.三角形相似的判定及其性质;2.平行线分线段成比例;3.切线的性质及判定

练习册系列答案
相关题目
 ,连接DE交BC于点F,AC=4,BC=3.求证:
,连接DE交BC于点F,AC=4,BC=3.求证:

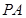 为圆
为圆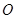 的切线,
的切线,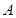 为切点,
为切点,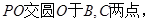
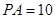 ,
,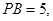
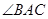 的角平分线与
的角平分线与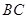 和圆
和圆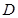 和
和
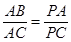 (2)求
(2)求 的值
的值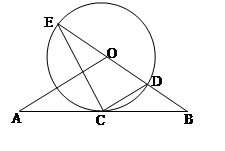
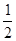 ,⊙O的半径为3,求OA的长.
,⊙O的半径为3,求OA的长.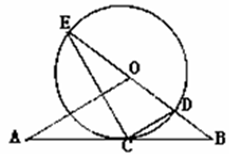
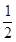 ,⊙O的半径为3,求OA的长.
,⊙O的半径为3,求OA的长. ,且AB是的
,且AB是的
 切⊙
切⊙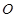 于点E,割线PBA交⊙
于点E,割线PBA交⊙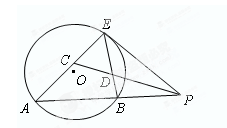
 ; (Ⅱ)
; (Ⅱ)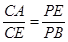 .
.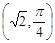 ,直线
,直线 的极坐标方程为
的极坐标方程为 ,且点A在直线
,且点A在直线 的值及直线
的值及直线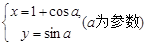 ,试判断直线l与圆C的位置关系.
,试判断直线l与圆C的位置关系.