题目内容
用数学归纳法证明不等式

证明略
(1)当n=1时,左=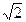 ,右=2,不等式成立
,右=2,不等式成立
(2)假设当n=k时等式成立,即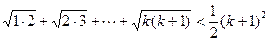
则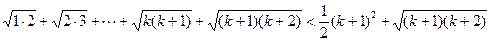
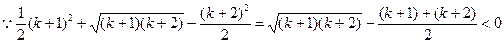
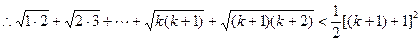
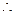 当n=k+1时, 不等式也成立
当n=k+1时, 不等式也成立
综合(1)(2),等式对所有正整数都成立
【名师指引】(1)数学归纳法证明命题,格式严谨,必须严格按步骤进行;
(2)归纳递推是证明的难点,应看准“目标”进行变形;
(3)由k推导到k+1时,有时可以“套”用其它证明方法,如:比较法、分析法等,表现出数学归纳法“灵活”的一面
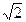 ,右=2,不等式成立
,右=2,不等式成立(2)假设当n=k时等式成立,即
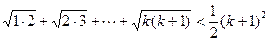
则
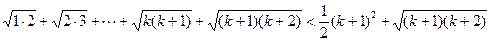
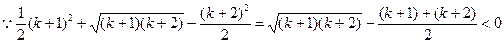
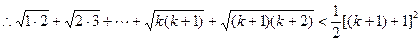
 当n=k+1时, 不等式也成立
当n=k+1时, 不等式也成立综合(1)(2),等式对所有正整数都成立
【名师指引】(1)数学归纳法证明命题,格式严谨,必须严格按步骤进行;
(2)归纳递推是证明的难点,应看准“目标”进行变形;
(3)由k推导到k+1时,有时可以“套”用其它证明方法,如:比较法、分析法等,表现出数学归纳法“灵活”的一面

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
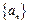 的前
的前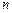 项和
项和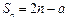 ,先计算数列的前4项,后猜想
,先计算数列的前4项,后猜想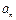 并证明之.
并证明之.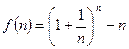 ,其中
,其中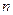 为正整数.
为正整数. ,
,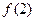 ,
,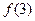 的值;
的值; 的正整数
的正整数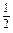 an·(4-an)(n∈N).
an·(4-an)(n∈N).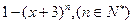 能被
能被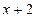 整除
整除 对一切正整数n都成立?证明你的结论
对一切正整数n都成立?证明你的结论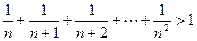 (
(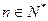 且
且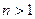 )
)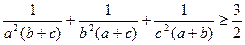 .
.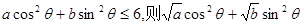 的最大值为 .
的最大值为 .