题目内容
9.已知P为抛物线y2=-6x上一个动点,Q为圆${x^2}+{(y-6)^2}=\frac{1}{4}$上一个动点,那么点P到点Q的距离与点P到y轴距离之和的最小值是( )| A. | $\frac{{3\sqrt{17}-7}}{2}$ | B. | $\frac{{3\sqrt{17}-4}}{2}$ | C. | $\frac{{3\sqrt{17}-1}}{2}$ | D. | $\frac{{3\sqrt{17}+1}}{2}$ |
分析 先根据抛物线方程求得焦点坐标,根据圆的方程求得圆心坐标,根据抛物线的定义可知P到准线的距离等于点P到焦点的距离,进而问题转化为求点P到点Q的距离与点P到抛物线的焦点距离之和的最小值,根据图象可知当P,Q,F三点共线时P到点Q的距离与点P到抛物线的y轴距离之和的最小,为圆心到焦点F的距离减去圆的半径减去y轴与准线的距离.
解答 解:由于P为抛物线y2=-6x上一个动点,Q为圆${x^2}+{(y-6)^2}=\frac{1}{4}$上一个动点,那么点P到点Q的距离与点P到y轴距离之和的最小值,可结合抛物线的定义,P到y轴距离为P到焦点距离减去$\frac{3}{2}$,
则最小值为抛物线的焦点到圆心的距离减去半径和$\frac{3}{2}$,
即为$\frac{3\sqrt{17}-4}{2}$,
故选B.
点评 本题主要考查了抛物线的定义的应用.考查了学生转化和化归,数形结合等数学思想.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
14.函数y=$\frac{x}{x+1}$的图象是( )
| A. |  | B. |  | C. |  | D. | 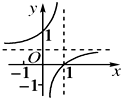 |
19.已知数列1,$\sqrt{3},\sqrt{5},\sqrt{7},3,\sqrt{11},…\sqrt{2n-1}$,则5是这个数列的( )
| A. | 第12项 | B. | 第13项 | C. | 第14项 | D. | 第25项 |
 在三棱锥A-BCD中,底面BCD是正三角形,AC=BD=2,AB=AD=$\sqrt{2}$,O为BC的中点.
在三棱锥A-BCD中,底面BCD是正三角形,AC=BD=2,AB=AD=$\sqrt{2}$,O为BC的中点. 如图所示,点B在以PA为直径的圆周上,点C在线段AB上,已知PA=5,PB=3,PC=$\frac{15\sqrt{2}}{7}$,设∠APB=α,∠APC=β,α,β均为锐角,则角β的值为$\frac{π}{4}$.
如图所示,点B在以PA为直径的圆周上,点C在线段AB上,已知PA=5,PB=3,PC=$\frac{15\sqrt{2}}{7}$,设∠APB=α,∠APC=β,α,β均为锐角,则角β的值为$\frac{π}{4}$.