题目内容
【题目】在直角坐标系![]() 中,椭圆
中,椭圆![]() 关于坐标轴对称,以坐标原点
关于坐标轴对称,以坐标原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系,
轴的正半轴为极轴建立极坐标系, ![]() ,
, ![]() 为椭圆
为椭圆![]() 上两点.
上两点.
(1)求直线![]() 的直角坐标方程与椭圆
的直角坐标方程与椭圆![]() 的参数方程;
的参数方程;
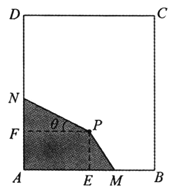
(2)若点![]() 在椭圆
在椭圆![]() 上,且点
上,且点![]() 在第一象限内,求四边形
在第一象限内,求四边形![]() 面积
面积![]() 的最大值.
的最大值.
【答案】(1)直角方程![]() 参数方程为
参数方程为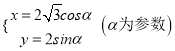 (2)6.
(2)6.
【解析】试题分析:
(1)将点A的坐标化为直角坐标便可得到直线![]() 的倾斜角,进而可得直线的方程;然后根据待定系数法可得椭圆的直角坐标方程,再化为参数方程即可.(2)由(1)可得点M(2
的倾斜角,进而可得直线的方程;然后根据待定系数法可得椭圆的直角坐标方程,再化为参数方程即可.(2)由(1)可得点M(2![]() cosα,2sinα) ,0<α<
cosα,2sinα) ,0<α<![]() ,进而可得点M到直线OA的距离d,所以S=S△MOA+S△MOB
,进而可得点M到直线OA的距离d,所以S=S△MOA+S△MOB
=6sin(α+![]() ),结合三角知识可得结果.
),结合三角知识可得结果.
试题解析:
(1)由A(![]() ,
,![]() )得直线OA的倾斜角为
)得直线OA的倾斜角为![]() ,
,
所以直线OA斜率为tan![]() =-1,
=-1,
故直线OA的方程为![]() ,即x+y=0.
,即x+y=0.
由x=ρcosα,y=ρsinα可得点A的直角坐标为(-![]() ,
, ![]() ),
),
因为椭圆C关于坐标轴对称,且B(2![]() ,0),
,0),
所以可设椭圆C:![]() +
+![]() =1,其中t>0且t≠12,
=1,其中t>0且t≠12,
将(-![]() ,
, ![]() )的坐标代入曲线C的方程,可得t=4,
)的坐标代入曲线C的方程,可得t=4,
故椭圆C的方程为![]() ,
,
所以椭圆C的参数方程为 .
.
(2)由(1)得M(2![]() cosα,2sinα),0<α<
cosα,2sinα),0<α<![]() .
.
点M到直线OA的距离d=![]() cosα+
cosα+![]() sinα.
sinα.
所以S=S△MOA+S△MOB=(3cosα+![]() sinα)+2
sinα)+2![]() sinα=3cosα+3
sinα=3cosα+3![]() sinα=6sin(α+
sinα=6sin(α+![]() ),
),
故当α=![]() 时,四边形OAMB面积S取得最大值6.
时,四边形OAMB面积S取得最大值6.

【题目】已知一工厂生产了某种产品700件,该工厂对这些产品进行了安全和环保这两个性能的质量检测。工厂决定利用随机数表法从中抽取100件产品进行抽样检测,现将700件产品按001,002,…,700进行编号;
(1)如果从第8行第4列的数开始向右读,请你依次写出最先检测的3件产品的编号;
(下面摘取了随机数表的第7~9行)
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
(2)抽取的100件产品的安全性能和环保性能的质量检测结果如下表:
检测结果分为优等、合格、不合格三个等级,横向和纵向分别表示安全性能和环保性能。若在该样本中,产品环保性能是优等的概率为![]() ,求
,求![]() ,
,![]() 的值。
的值。
件数 | 环保性能 | |||
优等 | 合格 | 不合格 | ||
安全性能 | 优等 | 6 | 20 | 5 |
合格 | 10 | 18 | 6 | |
不合格 |
| 4 |
| |
(3)已知![]() ,
,![]() ,求在安全性能不合格的产品中,环保性能为优等的件数比不合格的件数少的概率。
,求在安全性能不合格的产品中,环保性能为优等的件数比不合格的件数少的概率。
【题目】某书店销售刚刚上市的某高二数学单元测试卷,按事先拟定的价格进行5天试销,每种单价试销1天,得到如下数据:
单价x/元 | 18 | 19 | 20 | 21 | 22 |
销量y/册 | 61 | 56 | 50 | 48 | 45 |
(1)求试销![]() 天的销量的方差和
天的销量的方差和![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
附: 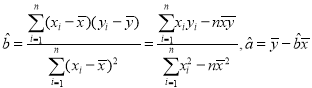 .
.
(2)预计以后的销售中,销量与单价服从上题中的回归直线方程,已知每册单元测试卷的成本是10元,为了获得最大利润,该单元测试卷的单价应定为多少元?