Question

在直三棱柱ABC-A₁B₁C₁中，已知AB=5，AC=4，BC=3，AA₁=4，点D在棱AB上．

(1)求证：AC⊥B₁C；
（2）若D是AB中点，求证：AC₁∥平面B₁CD.

Answer 1

(1)详见解析；（2）详见解析

解析试题分析：（1）要证明AC⊥B₁C，根据线面垂直的判定定理，只要转化证明AC⊥平面BB₁C₁C即可；
（2）要证明AC₁∥平面B₁CD，根据线面的判定定理，只要转换证明DE//AC₁即可.
试题解析：(1)证明：在△ABC中，因为AB=5，AC=4，BC=3，
所以AC²+BC²=AB²，所以AC⊥BC．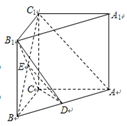

因为直三棱柱ABC-A₁B₁C₁，所以CC₁⊥AC，
因为BC∩AC=C，所以AC⊥平面BB₁C₁C．
所以AC⊥B₁C．   6分
（2）连结BC₁，交B₁C于E，连接DE．
因为直三棱柱ABC-A₁B₁C₁，D是AB中点，所以侧面BB₁C₁C为矩形，
DE为△ABC₁的中位线，所以DE//AC₁．
因为DE平面B₁CD，AC₁平面B₁CD，所以AC₁∥平面B₁CD．   12分
考点：空间位置关系的证明.