题目内容
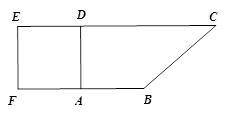
如图,在五面体ABCDEF中,四边形ABCD是矩形,DE⊥平面ABCD.
(1)求证:AB∥EF;
(2)求证:平面BCF⊥平面CDEF.
(1)详见解析,(2)详见解析.
解析试题分析:(1)证明线线平行,一般思路为利用线面平行的性质定理与判定定理进行转化. 因为四边形ABCD是矩形,所以AB∥CD,因为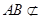 平面CDEF,
平面CDEF,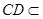 平面CDEF,所以AB∥平面CDEF.因为
平面CDEF,所以AB∥平面CDEF.因为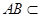 平面ABFE,平面
平面ABFE,平面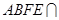 平面
平面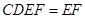 ,所以AB∥EF.(2)证明面面垂直,一般利用其判定定理证明,即先证线面垂直. 因为DE⊥平面ABCD,
,所以AB∥EF.(2)证明面面垂直,一般利用其判定定理证明,即先证线面垂直. 因为DE⊥平面ABCD, 平面ABCD,所以DE⊥BC.因为BC⊥CD,
平面ABCD,所以DE⊥BC.因为BC⊥CD,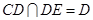 ,
,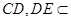 平面CDEF,所以BC⊥平面CDEF.因为BC
平面CDEF,所以BC⊥平面CDEF.因为BC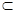 平面BCF,平面BCF⊥平面CDEF.
平面BCF,平面BCF⊥平面CDEF.
试题解析:【证】(1)因为四边形ABCD是矩形,所以AB∥CD,
因为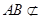 平面CDEF,
平面CDEF,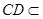 平面CDEF,
平面CDEF,
所以AB∥平面CDEF. 4分
因为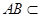 平面ABFE,平面
平面ABFE,平面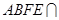 平面
平面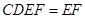 ,
,
所以AB∥EF. 7分
(2)因为DE⊥平面ABCD, 平面ABCD,
平面ABCD,
所以DE⊥BC. 9分
因为BC⊥CD,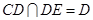 ,
,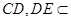 平面CDEF,
平面CDEF,
所以BC⊥平面CDEF. 12分
因为BC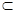 平面BCF,平面BCF⊥平面CDEF. 14分
平面BCF,平面BCF⊥平面CDEF. 14分
考点:线面平行与垂直关系

练习册系列答案
相关题目
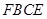 中, 四边形
中, 四边形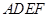 是正方形,
是正方形, ,
,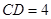 .将正方形沿
.将正方形沿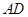 折起,得到如图2所示的多面体,其中面
折起,得到如图2所示的多面体,其中面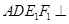 面
面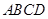 ,
,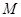 是
是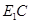 中点.
中点.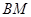 ∥平面
∥平面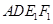 ;
;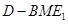 的体积.
的体积.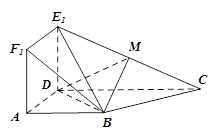


 为平行四边形,
为平行四边形,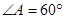 ,
,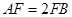 ,
,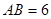 ,点
,点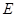 在
在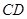 上,
上,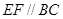 ,
, ,
,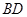 与
与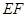 相交于
相交于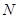 .现将四边形
.现将四边形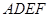 沿
沿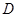 在平面
在平面 上的射影恰在直线
上的射影恰在直线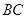 上.
上.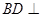 平面
平面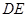 与平面
与平面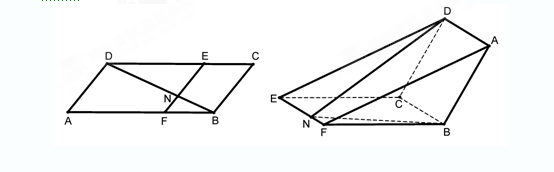
 中,
中, ,
,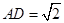 ,且
,且 ,以BD为折线,把△ABD折起,
,以BD为折线,把△ABD折起, ,连接AC.
,连接AC.
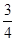 BC,且BG⊥GC,GB=GC=2,E是BC的中点,PG=4
BC,且BG⊥GC,GB=GC=2,E是BC的中点,PG=4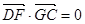 ,
,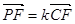 ,求
,求 的值.
的值.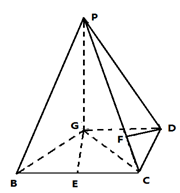

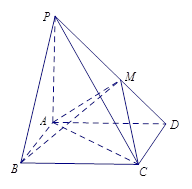
 中,底面
中,底面 是矩形,
是矩形,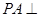 平面
平面 ,
,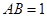 ,
,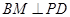 于点
于点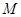 .
.

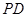 ;
; 与平面
与平面 所成的角的余弦值.
所成的角的余弦值.