题目内容
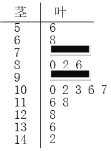
【题目】某校高三期中考试后,数学教师对本次全部学生的数学成绩按1∶20进行分层抽样,随机抽取了20名学生的成绩为样本,成绩用茎叶图记录如图所示,但部分数据不小心丢失,同时得到如下表所示的频率分布表:
分数段(分) |
|
|
|
|
| 总计 |
频数 |
| |||||
频率 |
| 0.25 |
(1)求表中![]() ,
,![]() 的值及成绩在
的值及成绩在![]()
![]() 范围内的样本数;
范围内的样本数;
(2)从成绩![]() 内的样本中随机抽取4个样本,设其中成绩在
内的样本中随机抽取4个样本,设其中成绩在![]() 内的样本个数为随机变量
内的样本个数为随机变量![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
(3)若把样本各分数段的频率看作总体相应各分数段的概率,现从全校高三期中考试数学成绩中随机抽取5个,求其中恰有2个成绩在![]() 内的概率.
内的概率.
【答案】(1)![]() ,
,![]() ,成绩在
,成绩在![]() ,
,![]() 范围内的样本数分别为2人,3人;(2)分布列见解析,
范围内的样本数分别为2人,3人;(2)分布列见解析,![]() ;(3)
;(3)![]() .
.
【解析】
(1)由茎叶图知成绩在[50,70)范围内的有2人,成绩在![]() 有
有![]() 人,在
人,在![]() 有
有![]() 人,即
人,即![]() ,根据茎叶图数据作差可得出成绩在
,根据茎叶图数据作差可得出成绩在![]()
![]() 范围内的样本数;
范围内的样本数;
(2)由茎叶图知成绩在![]() 内的共有8人,其中成绩在
内的共有8人,其中成绩在![]() 内的共有3人,于是X的可能取值为0,1,2,3,分别求出相应的概率,由此能求出X的分布列及数学期望E(X);
内的共有3人,于是X的可能取值为0,1,2,3,分别求出相应的概率,由此能求出X的分布列及数学期望E(X);
(3)该校高三期中考试数学成绩在![]() 的概率为
的概率为![]() ,设随机抽取5个,其中恰有2个成绩在
,设随机抽取5个,其中恰有2个成绩在![]() 的事件为
的事件为![]() ,由二项分布概率公式能求概率.
,由二项分布概率公式能求概率.
(1)由茎叶图知成绩在![]() 范围内的有
范围内的有![]() 人,得
人,得![]() ,
,
在![]() 有
有![]() 人,
人,
在![]() 有
有![]() 人,即
人,即![]() ,
,
在![]() 范围内的样本数为
范围内的样本数为![]() 人,
人,
在![]() 范围内的样本数为
范围内的样本数为![]() 人;
人;
(2)由茎叶图知成绩在![]() 内的共有
内的共有![]() 人,
人,
其中在![]() 内的共有
内的共有![]() 人,于是
人,于是![]() 的可能取值为0,1,2,3.
的可能取值为0,1,2,3.
得![]() ,
,![]() ,
,
![]() ,
,![]() .
.
得![]() 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
|
|
故![]() .
.
(3)该校高三期中考试数学成绩在![]() 的概率为
的概率为![]() ,
,
设随机抽取5个,其中恰有2个成绩在![]() 的事件为
的事件为![]() ,
,
则根据题设有![]() .
.

【题目】为保障食品安全,某地食品药监管部门对辖区内甲、乙两家食品企业进行检查,分别从这两家企业生产的某种同类产品中随机抽取了100件作为样本,并以样本的一项关键质量指标值为检测依据.已知该质量指标值对应的产品等级如下:
质量指标值 | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) | [40,45] |
等级 | 次品 | 二等品 | 一等品 | 二等品 | 三等品 | 次品 |
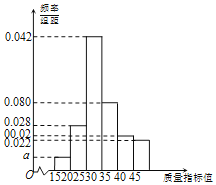
根据质量指标值的分组,统计得到了甲企业的样本频率分布直方图和乙企业的样本频数分布表(如下面表,其中a>0).
质量指标值 | 频数 |
[15,20) | 2 |
[20,25) | 18 |
[25,30) | 48 |
[30,35) | 14 |
[35,40) | 16 |
[40,45] | 2 |
合计 | 100 |
(Ⅰ)现从甲企业生产的产品中任取一件,试估计该件产品为次品的概率;
(Ⅱ)为守法经营、提高利润,乙企业开展次品生产原因调查活动.已知乙企业从样本里的次品中随机抽取了两件进行分析,求这两件次品中恰有一件指标值属于[40,45]的产品的概率;
(Ⅲ)根据图表数据,请自定标准,对甲、乙两企业食品质量的优劣情况进行比较.