题目内容
1.求下列动圆的圆心M的轨迹方程.(1)与⊙C1:x2+(y-1)2=1与⊙C2:x2+(y+1)2=1都外切;
(2)与C1:(x+3)2+y2=9外切,与⊙C2:(x-3)2+y2=1内切.
分析 (1)两定圆的圆心分别是C1(0,1),C2,(0,-1),半径分别为1,1,则动圆圆心M的轨迹方程可求.
(2)设动圆圆心M(x,y),半径为r,则|MC1|=r+3,|MC2|=r-1,可得|MC1|-|MC2|=r+3-r+1=4<|C1C2|=6,利用双曲线的定义,即可求动圆圆心M的轨迹方程.
解答 解:(1)两定圆的圆心分别是C1(0,1),C2,(0,-1),半径分别为1,1.
∵所求圆与两个圆都外切,
∴点M的轨迹为x轴,方程为y=0(x≠0);
(2)设动圆圆心M的坐标为(x,y),半径为r,则|MC1|=r+3,|MC2|=r-1,
∴|MC1|-|MC2|=r+3-r+1=4<|C1C2|=6,
由双曲线的定义知,点M的轨迹是以C1、C2为焦点的双曲线的右支,且2a=4,a=2,
双曲线的方程为:$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{5}$=1(x≥2).
点评 本题考查了轨迹方程的求法,考查了圆与圆的位置关系,训练了利用定义求双曲线的方程,是中档题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
 中,曲线
中,曲线 的参数方程为
的参数方程为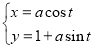 (
( 为参数,
为参数, ),在以坐标原点为极点,
),在以坐标原点为极点, 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线 .
. 的极坐标方程为
的极坐标方程为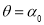 ,其中
,其中 满足
满足 ,若曲线
,若曲线 的公共点都在
的公共点都在 上,求
上,求 .
. 如图,四棱锥P-ABCD中底面是变长为a的正方形,且PD=a,PA=PC=$\sqrt{2}a$,求平面APB与平面PBD夹角的大小.
如图,四棱锥P-ABCD中底面是变长为a的正方形,且PD=a,PA=PC=$\sqrt{2}a$,求平面APB与平面PBD夹角的大小. 如图,在圆内接四边形ABCD中,AB∥DC,过点A作圆的切线与CB的延长线交于点E.若AB=AD=BC=5,AE=6,则BE=4DC=$\frac{25}{4}$.
如图,在圆内接四边形ABCD中,AB∥DC,过点A作圆的切线与CB的延长线交于点E.若AB=AD=BC=5,AE=6,则BE=4DC=$\frac{25}{4}$.