题目内容
5.观察下列各式:$\root{3}{2+\frac{2}{7}}$=2•$\root{3}{\frac{2}{7}}$,$\root{3}{3+\frac{3}{26}}$=3$•\root{3}{\frac{3}{26}}$,$\root{3}{4+\frac{4}{63}}$=4•$\root{3}{\frac{4}{63}}$,…,若$\root{3}{9+\frac{9}{m}}$=9•$\root{3}{\frac{9}{m}}$,则m=( )| A. | 80 | B. | 81 | C. | 728 | D. | 729 |
分析 观察每个等式可以发现每个被开方数的分数部分的分母是分子的立方减去1所得,从而可求m.
解答 解::$\root{3}{2+\frac{2}{7}}$=2•$\root{3}{\frac{2}{7}}$=2•$\root{3}{\frac{2}{{2}^{3}-1}}$,
$\root{3}{3+\frac{3}{26}}$=3$•\root{3}{\frac{3}{26}}=3•\root{3}{\frac{3}{{3}^{3}-1}}$,
,$\root{3}{4+\frac{4}{63}}$=4•$\root{3}{\frac{4}{63}}$=4$•\root{3}{\frac{4}{{4}^{3}-1}}$,
…,
所以$\root{3}{n+\frac{n}{{n}^{3}-1}}=n•\root{3}{\frac{n}{{n}^{3}-1}}$,
所以$\root{3}{9+\frac{9}{m}}$=9•$\root{3}{\frac{9}{m}}$=9$•\root{3}{\frac{9}{{9}^{3}-1}}$,
所以m=93-1=729-1=728;
故选C.
点评 本题考查了归纳推理,关键是由具体的前几个发现与序号的关系,总结出规律,猜想一般结论.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
17.下列说法正确的是( )
| A. | “x<0”是“ln(x+1)<0”的充要条件 | |
| B. | “?x≥2,x2-3x+2≥0”的否定是“?x<2,x2-3x+2<0” | |
| C. | 采用系统抽样法从某班按学号抽取5名同学参加活动,学号为5,16,27,38,49的同学均被选出,则该班学生人数可能为60 | |
| D. | 在某项测量中,测量结果X服从正态分布N(1,σ2)(σ>0),若X在(0,1)内取值的概率为0.4,则X在(0,2)内取值的概率为0.8 |
13.已知数列|an|,则an,an+1,an+2(n∈N+)成等比数列是“an+12=anan+2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
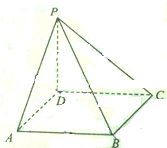 如图,四棱锥P-ABCD中底面是变长为a的正方形,且PD=a,PA=PC=$\sqrt{2}a$,求平面APB与平面PBD夹角的大小.
如图,四棱锥P-ABCD中底面是变长为a的正方形,且PD=a,PA=PC=$\sqrt{2}a$,求平面APB与平面PBD夹角的大小. 的连续可导函数
的连续可导函数 ,若满足以下两个条件:
,若满足以下两个条件: 没有零点,②对
没有零点,②对 ,都有
,都有 .
. 方程
方程 有( )个解.
有( )个解.