题目内容
.(本小题满分12分)
已知点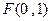 ,一动圆过点
,一动圆过点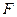 且与圆
且与圆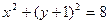 内切,
内切,
(1)求动圆圆心的轨迹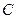 的方程;
的方程;
(2)设点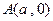 ,点
,点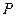 为曲线
为曲线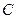 上任一点,求点
上任一点,求点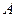 到点
到点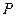 距离的最大值
距离的最大值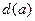 ;
;
(3)在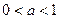 的条件下,设△
的条件下,设△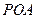 的面积为
的面积为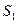 (
(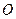 是坐标原点,
是坐标原点,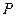 是曲线
是曲线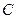 上横坐标为
上横坐标为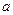 的点),以
的点),以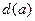 为边长的正方形的面积为
为边长的正方形的面积为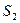 .若正数
.若正数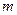 满足
满足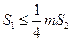 ,问
,问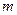 是否存在最小值,若存在,请求出此最小值,若不存在,请说明理由.
是否存在最小值,若存在,请求出此最小值,若不存在,请说明理由.
已知点
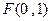 ,一动圆过点
,一动圆过点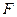 且与圆
且与圆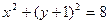 内切,
内切,(1)求动圆圆心的轨迹
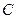 的方程;
的方程;(2)设点
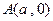 ,点
,点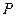 为曲线
为曲线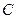 上任一点,求点
上任一点,求点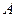 到点
到点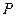 距离的最大值
距离的最大值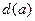 ;
;(3)在
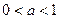 的条件下,设△
的条件下,设△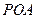 的面积为
的面积为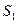 (
(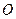 是坐标原点,
是坐标原点,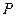 是曲线
是曲线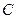 上横坐标为
上横坐标为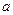 的点),以
的点),以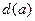 为边长的正方形的面积为
为边长的正方形的面积为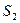 .若正数
.若正数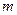 满足
满足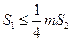 ,问
,问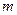 是否存在最小值,若存在,请求出此最小值,若不存在,请说明理由.
是否存在最小值,若存在,请求出此最小值,若不存在,请说明理由.解:(1)设圆心坐标为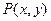 ,则动圆的半径为
,则动圆的半径为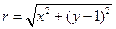 ,
,
又动圆与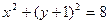 内切,所以有
内切,所以有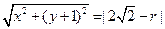 化简得
化简得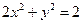
所以动圆圆心轨迹C的方程为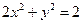 ;……………… 4分
;……………… 4分
(2)设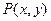 ,则
,则
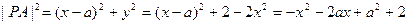
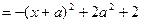 ,令
,令
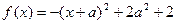 ,
,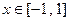
∴,当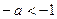 ,即
,即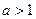 时
时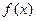 在
在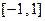 上是减函数,
上是减函数,
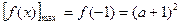 ;
;
当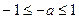 ,即
,即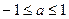 时,
时,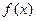 在
在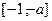 上是增函数,在
上是增函数,在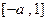 上是减函数,则
上是减函数,则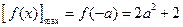 ;
;
当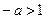 ,即
,即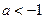 时,
时,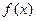 在
在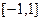 上是增函数,
上是增函数,
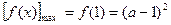 .
.
∴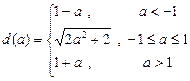 ………………… 8分
………………… 8分
(3)当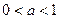 时,
时,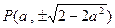 ,于是
,于是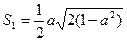 ,
,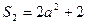 ,
,
若正数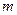 满足条件,则
满足条件,则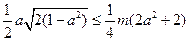 ,即
,即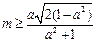 ,
,
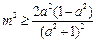 ,令
,令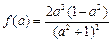 ,设
,设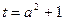 ,则
,则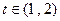 ,
,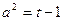 ,
,
于是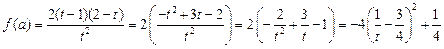 ,
,
∴当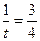 ,即
,即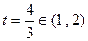 时,
时,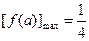 ,
,
即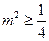 ,
,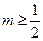 .∴
.∴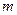 存在最小值
存在最小值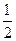 .………… 12分
.………… 12分
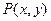 ,则动圆的半径为
,则动圆的半径为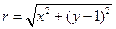 ,
,又动圆与
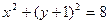 内切,所以有
内切,所以有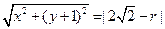 化简得
化简得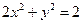
所以动圆圆心轨迹C的方程为
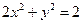 ;……………… 4分
;……………… 4分(2)设
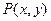 ,则
,则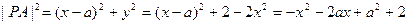
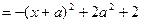 ,令
,令
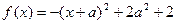 ,
,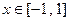
∴,当
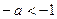 ,即
,即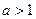 时
时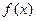 在
在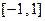 上是减函数,
上是减函数,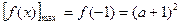 ;
;当
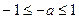 ,即
,即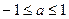 时,
时,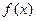 在
在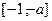 上是增函数,在
上是增函数,在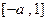 上是减函数,则
上是减函数,则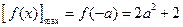 ;
;当
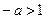 ,即
,即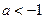 时,
时,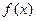 在
在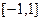 上是增函数,
上是增函数,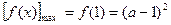 .
.∴
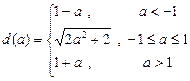 ………………… 8分
………………… 8分(3)当
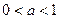 时,
时,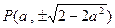 ,于是
,于是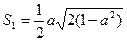 ,
,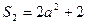 ,
,若正数
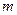 满足条件,则
满足条件,则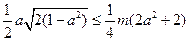 ,即
,即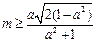 ,
,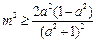 ,令
,令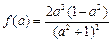 ,设
,设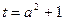 ,则
,则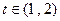 ,
,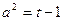 ,
,于是
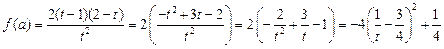 ,
,∴当
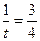 ,即
,即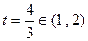 时,
时,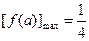 ,
,即
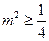 ,
,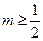 .∴
.∴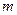 存在最小值
存在最小值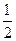 .………… 12分
.………… 12分略

练习册系列答案
相关题目
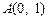 、
、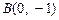 ,且
,且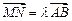 .
.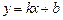 与曲线E交于不同的两点P、Q,且满足
与曲线E交于不同的两点P、Q,且满足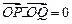 ,求实数
,求实数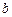 的取值范围。
的取值范围。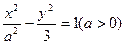 的两个焦点分别为
的两个焦点分别为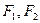 ,离心率为
,离心率为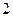 .
.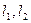 的方程;
的方程;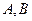 分别为
分别为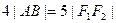 ,求线段
,求线段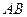 的中点
的中点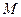 的轨迹方程,并说明轨迹是什么曲线.
的轨迹方程,并说明轨迹是什么曲线.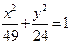 共焦点,且以
共焦点,且以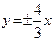 为渐近线,求双曲线方程
为渐近线,求双曲线方程 足条件
足条件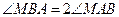 ,求动
,求动 点M的轨迹方程并指出轨迹是什么图形
点M的轨迹方程并指出轨迹是什么图形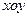 中,设点
中,设点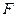 (1,0),直线
(1,0),直线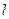 :
: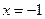 ,点
,点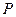 在直线
在直线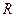 是线段
是线段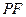 与
与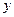 轴的交点,
轴的交点, 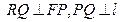 .
.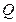 的轨迹的方程;
的轨迹的方程;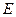 ,过点
,过点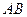 、
、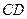 ,设
,设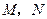 .求证:直线
.求证:直线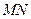 必过定点
必过定点 .
.

 上的动点
上的动点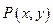 满足到点
满足到点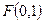 的距离比到直线
的距离比到直线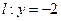 的距离小
的距离小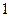 .
. 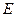 在直线
在直线 上,过点
上,过点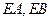 ,切点为
,切点为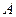 、
、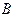 .
.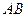 恒过一定点,并求出该定点的坐标;
恒过一定点,并求出该定点的坐标;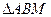 为等边三角形(
为等边三角形(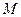 点也在直线
点也在直线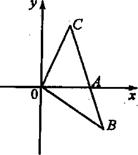
 分10分)
分10分)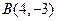 ,点
,点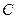 在第一象限内,
在第一象限内,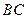 交
交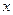 轴于点
轴于点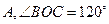 ,
,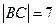 .
.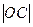 的长;
的长;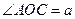 ,
,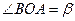 .(
.(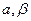 为锐角),求sina,sin
为锐角),求sina,sin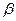 的值
的值