题目内容
将边长为1的正方形ABCD沿对角线AC对折成120°的二面角，则B、D在四面体A-BCD的外接球球面上的距离为 ．
【答案】分析：由边长为1的正方形ABCD沿对角线AC对折成120°的二面角，知四面体A-BCD的外接球半径R=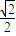
，B、D与球心所成的球心角n=120°，由此能求出B、D在四面体A-BCD的外接球球面上的距离．
解答：解：∵边长为1的正方形ABCD沿对角线AC对折成120°的二面角，
∴四面体A-BCD的外接球半径R=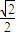
，
B、D与球心所成的球心角n=120°，
∴B、D在四面体A-BCD的外接球球面上的距离
d=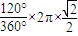
=
．
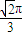故答案为：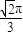
．
点评：本题考查球面距离的求法，解题时要认真审题，注意球半径的求法和二面角的应用．
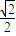，B、D与球心所成的球心角n=120°，由此能求出B、D在四面体A-BCD的外接球球面上的距离．解答：解：∵边长为1的正方形ABCD沿对角线AC对折成120°的二面角，
∴四面体A-BCD的外接球半径R=
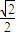，B、D与球心所成的球心角n=120°，
∴B、D在四面体A-BCD的外接球球面上的距离
d=
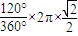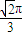=．故答案为：
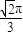．点评：本题考查球面距离的求法，解题时要认真审题，注意球半径的求法和二面角的应用．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
品学双优卷系列答案
相关题目
将边长为1的正方形ABCD沿对角线BD折起，使得点A到点A′的位置，且A′C=1，则折起后二面角A′-DC-B的大小（ ）
A、arctan
| ||||
B、
| ||||
C、arctan
| ||||
D、
|
将边长为1的正方形ABCD沿对角线BD折成直二面角，若点P满足| BP |
| 1 |
| 2 |
| BA |
| 1 |
| 2 |
| BC |
| BD |
| BP |
A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|