题目内容
设x、y∈R,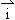 ,
, 为直角坐标平面内x,y轴正方向上的单位向量,若向量
为直角坐标平面内x,y轴正方向上的单位向量,若向量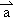 =x
=x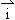 +(y+2)
+(y+2) ,
,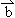 =x
=x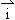 +(y-2)
+(y-2) ,且|
,且|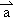 |+|
|+|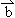 |=8.
|=8.
(1)求点M(x,y)的轨迹C的方程;
(2)过点(0,3)作直线l与曲线C交于A、B两点,设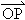 =
=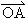 +
+ ,是否存在这样的直线l,使得四边形OAPB是矩形?若存在,求出直线l的方程;若不存在,试说明理由.
,是否存在这样的直线l,使得四边形OAPB是矩形?若存在,求出直线l的方程;若不存在,试说明理由.
答案:
解析:
解析:
|
(1)∵ ∴点M(x,y)到两个定点F1(0,-2),F2(0,2)的距离之和为8. ∴轨迹C为以F1,F2为焦点的椭圆,方程为 (2)∵l过y轴上的点(0,3). 若直线l是y轴,则A、B两点是椭圆的顶点. ∴ ∴直线l的斜率存在,设l的方程为y=kx+3,A(x1,y1)B(x2,y2) 由 此时Δ=(18k)2-4(4+3k2)(-21)>0恒成立. 且x1+x2=- ∵ 若存在直线l,使得四边形OAPB是矩形,则 ∵ 即(1+k2)x1x2+3k(x1+x2)+9=0 即(1+k2)·(- 即k2= ∴存在直线l:y=± |

练习册系列答案
 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
设x,y∈R,i为虚数单位,且
=1+2i,则Z=x+yi的共轭复数在复平面内对应的点在( )
| 3+4i |
| x+yi |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
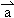 =x
=x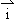 +(y+2)
+(y+2)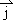 ,
,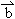 =x
=x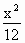 +
+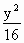 =1.
=1.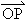 =
=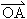 +
+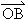 =
=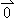 ,∴P与O重合,与四边形OAPB是矩形矛盾.
,∴P与O重合,与四边形OAPB是矩形矛盾.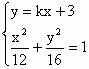 消去y得:(4+3k2)x2+18kx-21=0
消去y得:(4+3k2)x2+18kx-21=0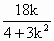 ,x1x2=-
,x1x2=-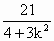 .
.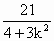 )+3k·(-
)+3k·(-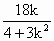 )+9=0
)+9=0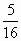 ,得k=±
,得k=±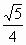
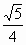 +3,使得四边形OAPB为矩形.
+3,使得四边形OAPB为矩形. ,
, 为直角坐标平面内x,y轴正方向上单位向量,若
为直角坐标平面内x,y轴正方向上单位向量,若 ,
, ,且
,且 .
.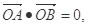 求证直线L与某个定圆E相切,并求出定圆E的方程。
求证直线L与某个定圆E相切,并求出定圆E的方程。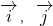 、为直角坐标系内x、y轴正方向上的单位向量,若
、为直角坐标系内x、y轴正方向上的单位向量,若 =x
=x +(y+2)
+(y+2) ,
, =x
=x ,是否存在直线l使四边形OAPB为正方形?若存在,求出l的方程,若不存在说明理由.
,是否存在直线l使四边形OAPB为正方形?若存在,求出l的方程,若不存在说明理由.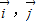 、为直角坐标系内x、y轴正方向上的单位向量,若
、为直角坐标系内x、y轴正方向上的单位向量,若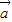 =x
=x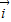 +(y+2)
+(y+2)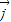 ,
,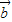 =x
=x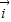 +(y-2)
+(y-2)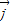 且
且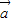 2+
2+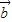 2=16.
2=16.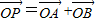 ,是否存在直线l使四边形OAPB为正方形?若存在,求出l的方程,若不存在说明理由.
,是否存在直线l使四边形OAPB为正方形?若存在,求出l的方程,若不存在说明理由.