题目内容
设x,y∈R,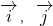 、为直角坐标系内x、y轴正方向上的单位向量,若
、为直角坐标系内x、y轴正方向上的单位向量,若 =x
=x +(y+2)
+(y+2) ,
, =x
=x +(y-2)
+(y-2) 且
且 2+
2+ 2=16.
2=16.
(1)求点M(x,y )的轨迹C的方程;
(2)过定点(0,3)作直线l与曲线C交于A、B两点,设 ,是否存在直线l使四边形OAPB为正方形?若存在,求出l的方程,若不存在说明理由.
,是否存在直线l使四边形OAPB为正方形?若存在,求出l的方程,若不存在说明理由.
解:(1)∵ =x
=x +(y+2)
+(y+2) ,
, =x
=x +(y-2)
+(y-2) 且
且 2+
2+ 2=16,
2=16,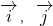 为直角坐标系内x、y轴正方向上的单位向量,
为直角坐标系内x、y轴正方向上的单位向量,
∴x2+(y+2)2+x2+(y-2)2=16
∴点M(x,y )的轨迹C的方程是x2+y2=4;
(2)假设存在直线l,设方程为y=kx+3,代入x2+y2=4可得(1+k2)x2+6kx+5=0
设A(x1,y1),B(x2,y2),则x1+x2=-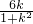 ,x1•x2=
,x1•x2=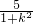
由题意, ,则x1•x2+y1•y2=0
,则x1•x2+y1•y2=0
∴x1•x2+k2x1•x2+3k(x1+x2)+9=0
∴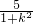 +
+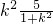 +3k•(-
+3k•(-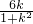 )+9=0
)+9=0
∴k=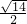
∴存在l且l的方程为y=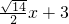 .
.
分析:(1)利用向量的数量积公式,即可求得点M(x,y )的轨迹C的方程;
(2)设出直线方程,代入圆的方程,结合韦达定理及向量的数量积公式,即可得到结论.
点评:本题考查轨迹方程,考查数量积公式的运用,考查直线与圆的位置关系,考查学生的计算能力,属于中档题.
 =x
=x +(y+2)
+(y+2) ,
, =x
=x +(y-2)
+(y-2) 且
且 2+
2+ 2=16,
2=16,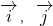 为直角坐标系内x、y轴正方向上的单位向量,
为直角坐标系内x、y轴正方向上的单位向量,∴x2+(y+2)2+x2+(y-2)2=16
∴点M(x,y )的轨迹C的方程是x2+y2=4;
(2)假设存在直线l,设方程为y=kx+3,代入x2+y2=4可得(1+k2)x2+6kx+5=0
设A(x1,y1),B(x2,y2),则x1+x2=-
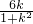 ,x1•x2=
,x1•x2=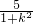
由题意,
 ,则x1•x2+y1•y2=0
,则x1•x2+y1•y2=0∴x1•x2+k2x1•x2+3k(x1+x2)+9=0
∴
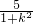 +
+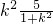 +3k•(-
+3k•(-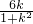 )+9=0
)+9=0∴k=
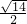
∴存在l且l的方程为y=
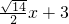 .
.分析:(1)利用向量的数量积公式,即可求得点M(x,y )的轨迹C的方程;
(2)设出直线方程,代入圆的方程,结合韦达定理及向量的数量积公式,即可得到结论.
点评:本题考查轨迹方程,考查数量积公式的运用,考查直线与圆的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
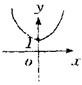
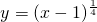 的反函数图象是
的反函数图象是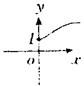
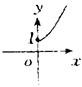
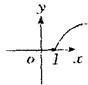
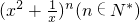 的二项展开式中第5项为常数项,则n=________.
的二项展开式中第5项为常数项,则n=________. -1=0绕点(1,
-1=0绕点(1, ax2+(1-a)x-1-lnx,a∈R.
ax2+(1-a)x-1-lnx,a∈R. 如图,圆内切于正方形,向该正方形内随机投掷N个点(假设N足够大,如N>1000),设落在阴影部分的点N1个,那么由随机模拟思想可得圆周率π的近似值为________.
如图,圆内切于正方形,向该正方形内随机投掷N个点(假设N足够大,如N>1000),设落在阴影部分的点N1个,那么由随机模拟思想可得圆周率π的近似值为________.