题目内容
（（本小题满分12分）设x，y∈R，
，
为直角坐标平面内x，y轴正方向上单位向量，若
向量
，
，且
．
（1）求点M（x，y）的轨迹C的方程；
（2）若直线L与曲线C交于A、B两点，若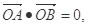
求证直线L与某个定圆E相切，并求出定圆E的方程。
【答案】
解：①∵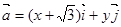
，
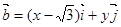，且
．
∴点M（x，y）到两个定点F1（
，0），F2（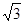
，0）的距离之和为
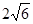∴点M的轨迹C是以F1、F2为焦点的椭圆，其方程为
………………………………………5分
②:当直线的斜率存在时，设直线为y=kx+m,A(x1,y1),B(x2,y2)，联立直线与椭圆的方程，
得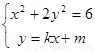
消去y并整理得
.
因为直线与椭圆有两个不同的交点，所以
…………(﹡)
,
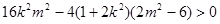
……………………7分
=
∵
∴
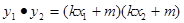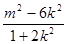
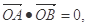
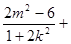
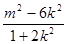=0
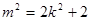满足(﹡)式，并且
，即原点到直线L的距离是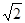
,
∴直线L与圆
相切。……………………………………………………10分
当直线的斜率不存在时，直线为x=m,
∴A(m,
),B(m,-),
∵
∴
, 
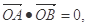
,直线L的方程是
,∴直线L与圆相切。
综合之得：直线L与圆相切。………………………………………12分
【解析】略
练习册系列答案
课时训练江苏人民出版社系列答案
黄冈经典趣味课堂系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
