题目内容
20.在△ABC中,a、b、c分别是角A、B、C的对边,且(2a+c)cosB=-bcosC(1)求角B的大小;
(2)若b=7,a+c=8,求a、c的值.
分析 (1)由正弦定理及三角函数恒等变换的应用化简已知等式可得:2sinAcosB=-sinA,结合sinA>0,即可解得B的值.
(2)利用余弦定理及(1)可得b2=49=64-ac,可得ac=15,结合a+c=8,即可求得a、c的值.
解答 解:(1)由正弦定理可得:(2sinA+sinC)cosB=-sinBcosC,
∴2sinAcosB=-sinBcosC-cosBsinC=-sin(B+C)=-sinA,
又∵sinA>0,∴$cosB=-\frac{1}{2}$,
∵B∈(0,π),
∴$B=\frac{2π}{3}$…(7分)
(2)b2=49=a2+c2-2accosB=a2+c2+ac=(a+c)2-ac=64-ac,
∴ac=15,
又∵a+c=8,∴$\left\{\begin{array}{l}a=3\\ c=5\end{array}\right.或\left\{\begin{array}{l}a=5\\ c=3\end{array}\right.$…(14分)
点评 本题主要考查了正弦定理,余弦定理及三角函数恒等变换的应用,属于基础题.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
11.已知f(x)=2x3-6x2+m(m为常数)在[-2,2]上有最大值3,那么此函数在[-2,2]上的最小值为( )
| A. | -5 | B. | -11 | C. | -29 | D. | -37 |
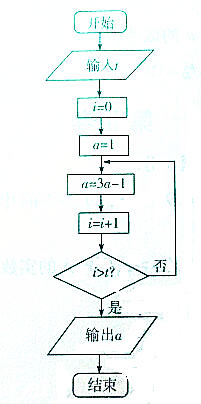 如图是一个程序框图,若输出a的值为365,则输入的t的值可以为5.
如图是一个程序框图,若输出a的值为365,则输入的t的值可以为5.