题目内容
设定义在R上的函数f(x)=
，若关于x的方程f2（x）+af（x）+b=0有3个不同实数解x1、x2、x3，且x1＜x2＜x3，则下列说法中错误的是（ ）
|
分析：关于x的方程f2（x）+af（x）+b=0有3个解，则必然含有x=1这样一个解，另外2个则在分段函数的另一段里面，刚好它是个绝对值函数，可以提供2个不同自变量时为同一值．既然含有x=1的解，此时f（1）=1，我们知道另外2个值也是1的肯定也能满足方程，所以关于x的方程f2（x）+af（x）+b=0有3个不同实数解时，f（x）=1，从而可得结论．
解答：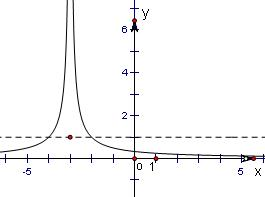
解：分段函数的图象如图所示
由图可知，只有当f（x）=1时，它有三个根．
∵
=1时，x=-2或-4．
∴关于x的方程f2（x）+af（x）+b=0有且只有3个不同实数解时，
解分别是-4，-3，-2，且x1=-4，x2=-3，x3=-2，
∴x12+x22+x32=16+9+4=29，x1+x3=-6，
∵f（x）=1，∴1+a+b=0
∵a2-4b=a2+4a+4=（a+2）2≥0
∴D不正确
故选D．
解：分段函数的图象如图所示由图可知，只有当f（x）=1时，它有三个根．
∵
| 1 |
| |x+3| |
∴关于x的方程f2（x）+af（x）+b=0有且只有3个不同实数解时，
解分别是-4，-3，-2，且x1=-4，x2=-3，x3=-2，
∴x12+x22+x32=16+9+4=29，x1+x3=-6，
∵f（x）=1，∴1+a+b=0
∵a2-4b=a2+4a+4=（a+2）2≥0
∴D不正确
故选D．
点评：本题主要考查函数的零点与方程根的关系、函数的图象等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于中档题．
练习册系列答案
相关题目
设定义在R上的函数f（x）同时满足以下条件：①f（x+1）=-f（x）对任意的x都成立；②当x∈[0，1]时，f（x）=ex-e•cos
+m（其中e=2.71828…是自然对数的底数，m是常数）．记f（x）在区间[2013，2016]上的零点个数为n，则（ ）
| πx |
| 2 |
A、m=-
| ||
| B、m=1-e，n=5 | ||
C、m=-
| ||
| D、m=e-1，n=4 |