题目内容
10.在数列$\{{a_n}\}中,{a_1}=1,{a_{n+1}}=1-\frac{1}{{4{a_n}}},{b_n}=\frac{2}{{2{a_n}-1}},其中n∈{N^*}$.(1)求证:数列{bn}是等差数列,并求数列{an}的通项公式an;
(2)设cn=$\frac{4{a}_{n}}{n+1}$,数列{cncn+2}的前n项和为Tn,求证:Tn<3.
分析 (1)直接利用作差法结合数列递推式即可证明数列{bn}是等差数列,求出其通项公式后代入${b}_{n}=\frac{2}{2{a}_{n}-1}$得数列{an}的通项公式an;
(2)把数列{an}的通项公式an代入cn=$\frac{4{a}_{n}}{n+1}$,得到{cncn+2}的通项公式,然后利用裂项相消法求前n项和Tn,则答案得证.
解答 证明:(1)∵bn+1-bn=$\frac{2}{2{a}_{n+1}-1}-\frac{2}{2{a}_{n}-1}$
=$\frac{2}{2-(1-\frac{1}{4{a}_{n}})-1}-\frac{2}{2{a}_{n}-1}$=$\frac{4{a}_{n}}{2{a}_{n}-1}-\frac{2}{2{a}_{n}-1}$=2,
∴数列{bn}是等差数列,
∵a1=1,∴${b}_{1}=\frac{2}{2{a}_{1}-1}=2$,
∴bn=2+(n-1)×2=2n,
由${b}_{n}=\frac{2}{2{a}_{n}-1}$得,$2{a}_{n}-1=\frac{2}{{b}_{n}}$=$\frac{1}{n}$,
∴${a}_{n}=\frac{n+1}{2n}$;
(2)cn=$\frac{4{a}_{n}}{n+1}$=$\frac{4•\frac{n+1}{2n}}{n+1}=\frac{2}{n}$,
则cncn+2=$\frac{2}{n}•\frac{2}{n+2}=\frac{4}{n(n+2)}$=$2(\frac{1}{n}-\frac{1}{n+2})$,
∴${T}_{n}=2(1-\frac{1}{3}+\frac{1}{2}-\frac{1}{4}+\frac{1}{3}-\frac{1}{5}+…+\frac{1}{n}-\frac{1}{n+2})$
=$2(1+\frac{1}{2}-\frac{1}{n+1}-\frac{1}{n+2})$=3-$\frac{1}{n+1}-\frac{1}{n+2}$<3.
点评 本题考查了数列递推式,考查了等差关系的确定,训练了裂项相消法求数列的和,是中档题.

| A. | $\frac{1}{2}+\frac{1}{2}i$ | B. | $\frac{1}{2}+\frac{5}{2}i$ | C. | $\frac{3}{2}+\frac{1}{2}i$ | D. | $\frac{3}{2}+\frac{5}{2}i$ |
| A. | $\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | $\sqrt{6}$ |

| A. | $\frac{3}{4}$ | B. | $\frac{5}{8}$ | C. | $\frac{7}{8}$ | D. | $\frac{1}{2}$ |
| A. | $\frac{π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{2}{3}π$ | D. | $\frac{4}{3}π$ |
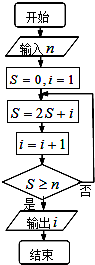
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |