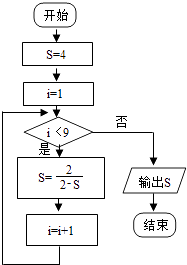
题目内容
【题目】已知复数z满足|z|=![]()
![]() 的虚部为2,z所对应的点在第一象限,
的虚部为2,z所对应的点在第一象限,
(1)求z;
(2)若z,z2,z-z2在复平面上对应的点分别为A,B,C,求cos∠ABC.
【答案】(1) z=1+i.
(2)![]()
【解析】分析:(1)设z=x+yi(x,y∈R),根据题意得到x,y的方程组,即得z.(2)先求z,z2,z-z2在复平面上对应的点,再利用向量的夹角公式求cos∠ABC.
详解:(1)设z=x+yi(x,y∈R).
∵|z|![]()
∴x2+y2=2. ①
又z2=(x+yi)2=x2-y2+2xyi,
∴2xy=2,∴xy=1. ②
由①②可![]()
∴z=1+i或z=-1-i.
又x>0,y>0,
∴z=1+i.
(2)z2=(1+i)2=2i,
z-z2=1+i-2i=1-i.
如图所示,
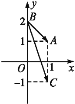
∴A(1,1),B(0,2),C(1,-1),
![]()
∴cos∠ABC![]()

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
【题目】为了了解创建文明城市过程中学生对创建工作的满意情况,相关部门对某中学的100名学生进行调查.得到如下的统计表:
满意 | 不满意 | 合计 | |
男生 | 50 |
|
|
女生 |
| 15 |
|
合计 |
|
| 100 |
已知在全部100名学生中随机抽取1人对创建工作满意的概率为![]() .
.
(1)在上表中![]() 相应的数据依次为;
相应的数据依次为;
(2)是否有充足的证据说明学生对创建工作的满意情况与性别有关?