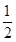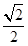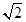题目内容
已知双曲线过点(3,-2),且与椭圆4x2+9y2=36有相同的焦点.
(1)求双曲线的标准方程;
(2)求以双曲线的右准线为准线的抛物线的标准方程.
(1)求双曲线的标准方程;
(2)求以双曲线的右准线为准线的抛物线的标准方程.
(1)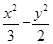 =1.(2)y2=-
=1.(2)y2=-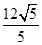 x.
x.
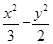 =1.(2)y2=-
=1.(2)y2=-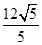 x.
x.(1)由题意,椭圆4x2+9y2=36的焦点为(±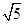 ,0),即c=
,0),即c=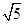 ,
,
∴设所求双曲线的方程为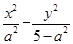 =1,∵双曲线过点(3,-2),
=1,∵双曲线过点(3,-2),
∴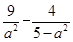 =1,∴a2=3或a2=15(舍去).故所求双曲线的方程为
=1,∴a2=3或a2=15(舍去).故所求双曲线的方程为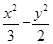 =1.
=1.
(2)由(1)可知双曲线的右准线为x=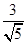 .设所求抛物线的标准方程为y2=-2px(p>0),则p=
.设所求抛物线的标准方程为y2=-2px(p>0),则p=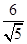 ,故所求抛物线的标准方程为y2=-
,故所求抛物线的标准方程为y2=-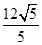 x.
x.
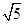 ,0),即c=
,0),即c=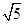 ,
,∴设所求双曲线的方程为
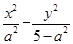 =1,∵双曲线过点(3,-2),
=1,∵双曲线过点(3,-2),∴
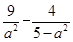 =1,∴a2=3或a2=15(舍去).故所求双曲线的方程为
=1,∴a2=3或a2=15(舍去).故所求双曲线的方程为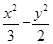 =1.
=1.(2)由(1)可知双曲线的右准线为x=
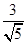 .设所求抛物线的标准方程为y2=-2px(p>0),则p=
.设所求抛物线的标准方程为y2=-2px(p>0),则p=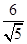 ,故所求抛物线的标准方程为y2=-
,故所求抛物线的标准方程为y2=-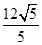 x.
x.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
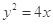 的焦点到双曲线
的焦点到双曲线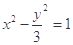 的渐近线的距离是( ).
的渐近线的距离是( ).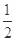
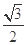
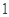
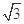
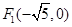 ,点P在双曲线上,且线段
,点P在双曲线上,且线段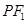 的中点坐标为(0,2),则此双曲线的方程是________________.
的中点坐标为(0,2),则此双曲线的方程是________________. 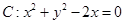 的圆心到双曲线
的圆心到双曲线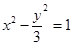 的渐近线的距离是( )
的渐近线的距离是( )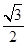
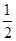
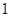
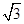
 =1(a>0,b>0)与抛物线y2=8x有一个公共的焦点F,且两曲线的一个交点为P,若PF=5,则双曲线的渐近线方程为________.
=1(a>0,b>0)与抛物线y2=8x有一个公共的焦点F,且两曲线的一个交点为P,若PF=5,则双曲线的渐近线方程为________.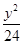 =1的两个焦点,P是双曲线上的一点,且3PF1=4PF2,则△PF1F2的面积等于________.
=1的两个焦点,P是双曲线上的一点,且3PF1=4PF2,则△PF1F2的面积等于________.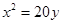 的焦点重合,且其渐近线的方程为
的焦点重合,且其渐近线的方程为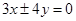 ,则该双曲线的标准方程为
,则该双曲线的标准方程为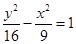
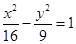
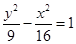
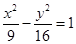
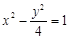 有共同的渐近线,且经过点P(1,4)的双曲线方程为 ( )
有共同的渐近线,且经过点P(1,4)的双曲线方程为 ( )