题目内容
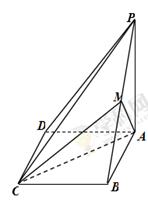
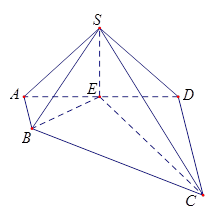
如图,在四棱锥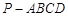 中,
中, 为平行四边形,且
为平行四边形,且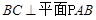 ,
,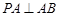 ,
,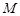 为
为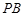 的中点,
的中点,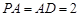 ,
,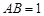 .
.
(Ⅰ)求证: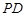 //
//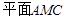 ;
;
(Ⅱ)求三棱锥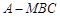 的高.
的高.
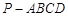 中,
中, 为平行四边形,且
为平行四边形,且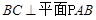 ,
,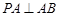 ,
,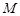 为
为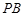 的中点,
的中点,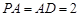 ,
,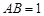 .
.
(Ⅰ)求证:
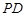 //
//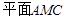 ;
;(Ⅱ)求三棱锥
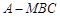 的高.
的高.(Ⅰ)详见解析;(Ⅱ)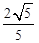 .
.
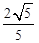 .
.试题分析:(Ⅰ)连接
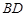 ,设
,设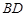 与
与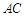 相交于点
相交于点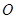 ,连接
,连接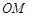 ,根据
,根据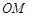 为
为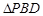 的中位线便可得出结论;(Ⅱ)由条件证明
的中位线便可得出结论;(Ⅱ)由条件证明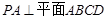 ,
,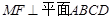 ,再 利用等体积法求得,即
,再 利用等体积法求得,即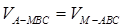 .
.试题解析:
(Ⅰ)证明:连接
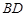 ,设
,设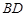 与
与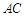 相交于点
相交于点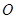 ,连接
,连接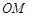 ,
,∵ 四边形
 是平行四边形,∴点
是平行四边形,∴点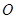 为
为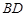 的中点.
的中点.∵
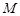 为
为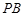 的中点, ∴
的中点, ∴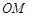 为
为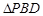 的中位线,
的中位线,∴
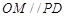 . 2分
. 2分∵
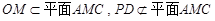 ,
,∴
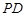 //
//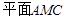 . 4分
. 4分(Ⅱ)解:∵
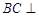 平面
平面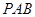 ,
,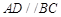 ,
,则
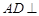 平面
平面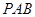 ,故
,故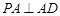 ,
,又
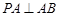 , 且
, 且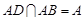 ,
,∴
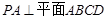 . 8分
. 8分取
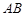 的中点
的中点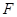 ,连接
,连接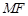 ,则
,则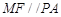 ,
,∴
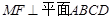 ,且
,且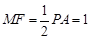 . 9分
. 9分设三棱锥
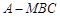 的高为
的高为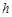 ,由
,由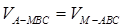 ,
,有
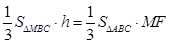 ,得
,得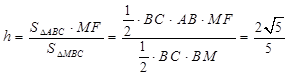 . 12分
. 12分
练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
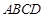 是菱形,
是菱形,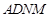 是矩形,平面
是矩形,平面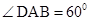 ,
,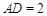 ,
,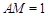 ,
,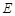 是
是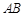 的中点.
的中点.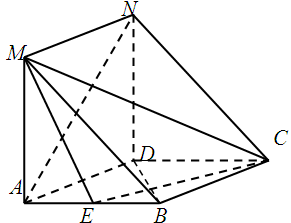
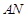 //平面
//平面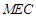 ;
;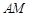 上是否存在点
上是否存在点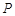 ,使二面角
,使二面角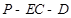 的大小为
的大小为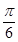 ?若存在,求出
?若存在,求出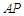 的长
的长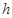 ;若不存在,请说明理由.
;若不存在,请说明理由.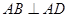 ,
,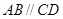 ,
,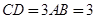 ,平面
,平面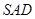 ⊥平面
⊥平面 ,
,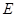 是线段
是线段 上一点,
上一点,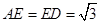 ,
,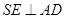 .
.
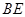 ⊥平面
⊥平面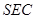 ;
;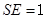 ,求直线
,求直线 与平面
与平面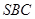 所成角的正弦值.
所成角的正弦值.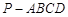 中,侧面
中,侧面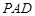 是正三角形,底面
是正三角形,底面 是边长为2的正方形,侧面
是边长为2的正方形,侧面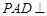 平面
平面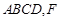 为
为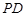 的中点.
的中点.
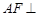 平面
平面 ;
;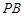 与平面
与平面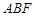 所成角的正切值.
所成角的正切值.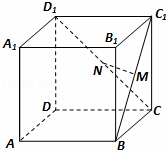
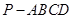 中,点
中,点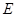 为
为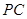 中点,则下列命题正确的是( )
中点,则下列命题正确的是( )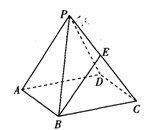
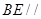 面
面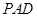 ,且直线
,且直线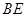 到面
到面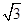
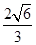
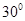
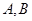 为 正方体的两个顶点,
为 正方体的两个顶点,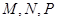 分别为其所在棱的中点,能得出
分别为其所在棱的中点,能得出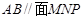 的图形的序号是______.
的图形的序号是______.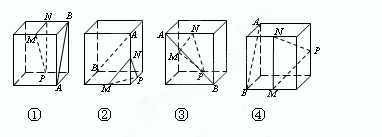
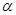 外有两条直线
外有两条直线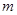 和
和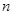 ,如果
,如果 和
和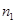 ,给出下列四个命题:①
,给出下列四个命题:① ②
② ③
③