题目内容
已知函数y=f(x)(x∈D),方程f(x)=x的根x称为函数f(x)的不动点;若a1∈D,an+1=f(an)(n∈N*),则称{an} 为由函数f(x)导出的数列.设函数g(x)=
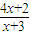 ,h(x)=
,h(x)=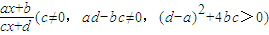
(1)求函数g(x)的不动点x1,x2;
(2)设a1=3,{an} 是由函数g(x)导出的数列,对(1)中的两个不动点x1,x2(不妨设x1<x2),数列求证
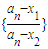 是等比数列,并求
是等比数列,并求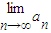 ;
;(3)试探究由函数h(x)导出的数列{bn},(其中b1=p)为周期数列的充要条件.
注:已知数列{bn},若存在正整数T,对一切n∈N*都有bn+T=bn,则称数列{bn} 为周期数列,T是它的一个周期.
【答案】分析:(1)直接解方程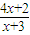 =x,求出对应的自变量的值即可;
=x,求出对应的自变量的值即可;
(2)直接把上面的结论代入并设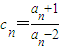 ,求出cn+1的表达式即可证明求证
,求出cn+1的表达式即可证明求证 是等比数列;进而求出{an} 的通项公式,即可求
是等比数列;进而求出{an} 的通项公式,即可求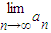 ;
;
(3)先利用h(x)= =x,得方程有两个不相等的实数根x1,x2;再求出{
=x,得方程有两个不相等的实数根x1,x2;再求出{ }是等比数列,首项为
}是等比数列,首项为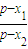 ,公比为
,公比为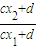 ;即可找到由函数h(x)导出的数列{bn}(其中b1=p)为周期数列的充要条件.
;即可找到由函数h(x)导出的数列{bn}(其中b1=p)为周期数列的充要条件.
解答:解:(1)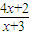 =x,即x2-x-2=0,得x1=-1,x2=2,
=x,即x2-x-2=0,得x1=-1,x2=2,
所以函数g(x)的不动点为x1=-1,x2=2.
(2):a1=3,an+1=g(an)=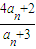 ,设cn=
,设cn= ,
,
则cn+1=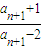 =
=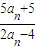 =
=
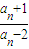 =
= cn,c1=
cn,c1= =4.
=4.
所以数列{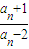 }是等比数列,公比为
}是等比数列,公比为 ,首项为4.
,首项为4.
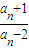 =4•
=4• 得an=
得an=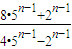 .
.
 =
=
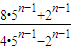 =
=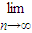
 =2.
=2.
(3):h(x)= =x,即cx2+(d-a)x-b=0.
=x,即cx2+(d-a)x-b=0.
因为△=(d-a)2+4ac>0,所以该方程有两个不相等的实数根x1,x2.
b1=p,bn+1=h(bn)= ,
,
 =
= =
= •
•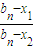 ,
,
则{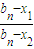 }是等比数列,首项为
}是等比数列,首项为 ,公比为
,公比为 .
.
因为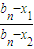 =
=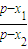 (
( )n-1,所以
)n-1,所以 =
= (
(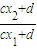 )n+T-1.
)n+T-1.
数列{bn}为周期数列的充要条件是(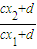 )n-1=(
)n-1=(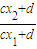 )n+T-1,即(
)n+T-1,即( )T=1.
)T=1.
故|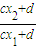 |=1,但x1≠x2,从而cx2+d=-cx1-d.x1+x2=-
|=1,但x1≠x2,从而cx2+d=-cx1-d.x1+x2=- =-
=-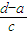 ,
,
故d=-a.
点评:本题主要考查数列知识和函数知识,属于难题.基础较弱的学生建议只做第一,第二问.
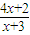 =x,求出对应的自变量的值即可;
=x,求出对应的自变量的值即可;(2)直接把上面的结论代入并设
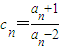 ,求出cn+1的表达式即可证明求证
,求出cn+1的表达式即可证明求证 是等比数列;进而求出{an} 的通项公式,即可求
是等比数列;进而求出{an} 的通项公式,即可求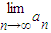 ;
;(3)先利用h(x)=
 =x,得方程有两个不相等的实数根x1,x2;再求出{
=x,得方程有两个不相等的实数根x1,x2;再求出{ }是等比数列,首项为
}是等比数列,首项为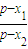 ,公比为
,公比为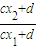 ;即可找到由函数h(x)导出的数列{bn}(其中b1=p)为周期数列的充要条件.
;即可找到由函数h(x)导出的数列{bn}(其中b1=p)为周期数列的充要条件.解答:解:(1)
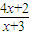 =x,即x2-x-2=0,得x1=-1,x2=2,
=x,即x2-x-2=0,得x1=-1,x2=2,所以函数g(x)的不动点为x1=-1,x2=2.
(2):a1=3,an+1=g(an)=
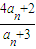 ,设cn=
,设cn= ,
,则cn+1=
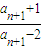 =
=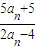 =
=
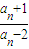 =
= cn,c1=
cn,c1= =4.
=4.所以数列{
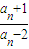 }是等比数列,公比为
}是等比数列,公比为 ,首项为4.
,首项为4.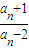 =4•
=4• 得an=
得an=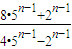 .
. =
=
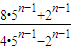 =
=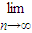
 =2.
=2.(3):h(x)=
 =x,即cx2+(d-a)x-b=0.
=x,即cx2+(d-a)x-b=0.因为△=(d-a)2+4ac>0,所以该方程有两个不相等的实数根x1,x2.
b1=p,bn+1=h(bn)=
 ,
, =
= =
= •
•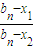 ,
,则{
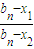 }是等比数列,首项为
}是等比数列,首项为 ,公比为
,公比为 .
.因为
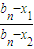 =
=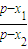 (
( )n-1,所以
)n-1,所以 =
= (
(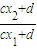 )n+T-1.
)n+T-1.数列{bn}为周期数列的充要条件是(
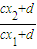 )n-1=(
)n-1=(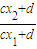 )n+T-1,即(
)n+T-1,即( )T=1.
)T=1.故|
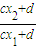 |=1,但x1≠x2,从而cx2+d=-cx1-d.x1+x2=-
|=1,但x1≠x2,从而cx2+d=-cx1-d.x1+x2=- =-
=-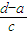 ,
,故d=-a.
点评:本题主要考查数列知识和函数知识,属于难题.基础较弱的学生建议只做第一,第二问.

练习册系列答案
相关题目
 已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为
已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为 已知函数y=f(x)的图象如图,则满足
已知函数y=f(x)的图象如图,则满足