题目内容
设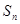 是各项均为非零实数的数列
是各项均为非零实数的数列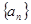 的前
的前 项和,给出如下两个命题上:
项和,给出如下两个命题上:
命题 :
: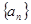 是等差数列;命题
是等差数列;命题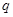 :等式
:等式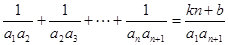 对任意
对任意 (
(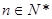 )恒成立,其中
)恒成立,其中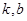 是常数。
是常数。
⑴若 是
是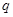 的充分条件,求
的充分条件,求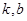 的值;
的值;
⑵对于⑴中的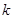 与
与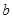 ,问
,问 是否为
是否为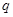 的必要条件,请说明理由;
的必要条件,请说明理由;
⑶若 为真命题,对于给定的正整数
为真命题,对于给定的正整数 (
(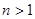 )和正数M,数列
)和正数M,数列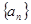 满足条件
满足条件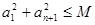 ,试求
,试求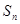 的最大值。
的最大值。
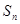 是各项均为非零实数的数列
是各项均为非零实数的数列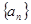 的前
的前 项和,给出如下两个命题上:
项和,给出如下两个命题上:命题
 :
: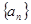 是等差数列;命题
是等差数列;命题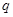 :等式
:等式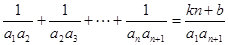 对任意
对任意 (
(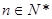 )恒成立,其中
)恒成立,其中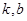 是常数。
是常数。⑴若
 是
是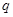 的充分条件,求
的充分条件,求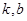 的值;
的值;⑵对于⑴中的
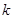 与
与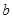 ,问
,问 是否为
是否为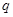 的必要条件,请说明理由;
的必要条件,请说明理由;⑶若
 为真命题,对于给定的正整数
为真命题,对于给定的正整数 (
(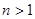 )和正数M,数列
)和正数M,数列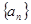 满足条件
满足条件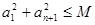 ,试求
,试求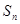 的最大值。
的最大值。(1)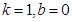 ;(2)是,证明见解析;(3)
;(2)是,证明见解析;(3)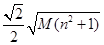 .
.
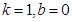 ;(2)是,证明见解析;(3)
;(2)是,证明见解析;(3)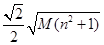 .
.试题分析:(1)
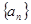 是等差数列,和
是等差数列,和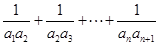 可以用裂项相消法求出,等式
可以用裂项相消法求出,等式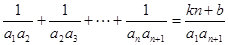 就变为关于
就变为关于 的恒等式,利用恒等式的知识可求出
的恒等式,利用恒等式的知识可求出 ;(2)等式
;(2)等式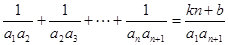 对任意
对任意 (
(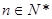 )恒成立,等式左边是一个和式,相当于一个新数列的前
)恒成立,等式左边是一个和式,相当于一个新数列的前 项和,处理方法是把式子中的
项和,处理方法是把式子中的 用
用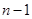 代换后,两式相减,本题中得到
代换后,两式相减,本题中得到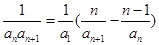 ,这个式子可整理为
,这个式子可整理为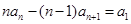 ,这是关于
,这是关于 的恒等式,因此
的恒等式,因此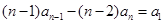
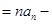
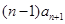 ,即
,即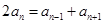 , 这就说明
, 这就说明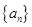 为等差数列,得证,解题时还要注意对
为等差数列,得证,解题时还要注意对 的初始值是否成立;(3)已知条件为等差数列
的初始值是否成立;(3)已知条件为等差数列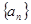 中
中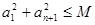 ,要求
,要求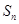 的最大值,为了能对数列
的最大值,为了能对数列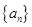 进行处理,我们利用三角换元法,对已知条件变换,设设
进行处理,我们利用三角换元法,对已知条件变换,设设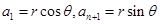 ,(
,(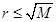 ),这样数列的公差
),这样数列的公差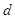 就可求出,从而也就能求出前
就可求出,从而也就能求出前 项和
项和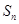 ,
,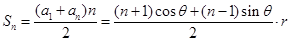 ,再利用三角函数
,再利用三角函数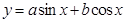 的最大值为
的最大值为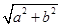 ,就能求出
,就能求出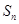 的最大值.
的最大值.试题解析:(1)设
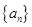 的公差为
的公差为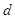 ,则原等式可化为
,则原等式可化为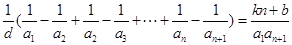 ,所以
,所以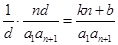 ,
,即
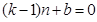 对于
对于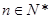 恒成立,所以
恒成立,所以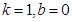 . 4分
. 4分(2)当
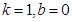 时,假设
时,假设 为
为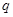 的必要条件,即“若
的必要条件,即“若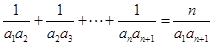 ①对于任意的
①对于任意的 (
(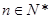 )恒成立,则
)恒成立,则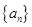 为等差数列”,
为等差数列”,当
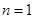 时,
时,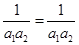 显然成立, 6分
显然成立, 6分当
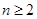 时,
时,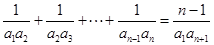 ②,由①-②得:
②,由①-②得: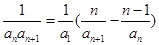 ,
,即
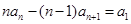 ③,
③,当
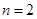 时,
时,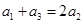 ,即
,即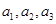 成等差数列,
成等差数列,当
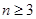 时,
时,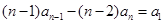 ④,由③④得
④,由③④得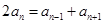 ,所以
,所以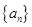 为等差数列,即
为等差数列,即 是
是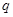 的必要条件. 10分
的必要条件. 10分(3)由
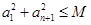 ,可设
,可设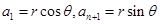 ,所以
,所以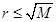 .
.设数列
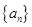 的公差为
的公差为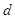 ,则
,则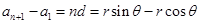 ,所以
,所以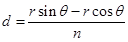 ,
,所以
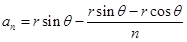 ,
,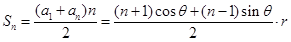
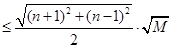
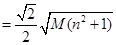 ,
,所以
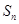 的最大值为
的最大值为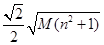 . 16分
. 16分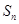 的最大值问题.
的最大值问题.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
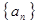 ,满足
,满足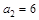 ,
,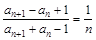
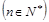 ,
, ,求数列
,求数列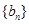 所满足的通项公式;
所满足的通项公式;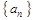 的通项公式;
的通项公式;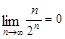 ,设
,设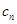 =
=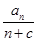
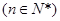 ,常数
,常数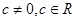 ,若数列
,若数列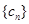 是等差数列,记
是等差数列,记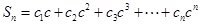 ,求
,求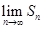 .
.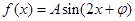
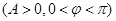 ,当
,当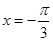 时取得最小值-4.
时取得最小值-4.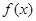 的解析式;
的解析式;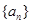 前n项和为
前n项和为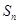 ,且
,且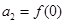 ,
,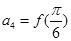 ,求数列
,求数列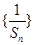 的前n项和
的前n项和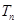 .
.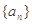 中,公差
中,公差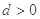 ,其前
,其前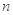 项和为
项和为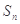 ,且满足:
,且满足: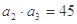 ,
,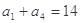 .
.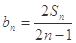 ,
,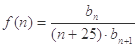 (
(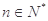 ),求
),求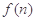 的最大值.
的最大值.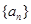 的前
的前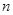 项和为
项和为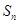 ,且
,且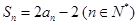 ,数列
,数列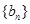 满足
满足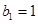 ,且
,且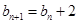 .
. 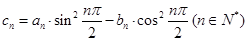 ,求数列
,求数列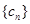 的前
的前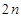 项和
项和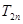 .
. 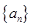 中,
中,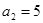 ,
,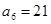 ,记数列
,记数列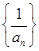 的前
的前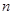 项和为
项和为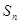 ,若
,若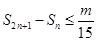 对
对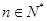 恒成立,则正整数
恒成立,则正整数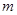 的最小值为( )
的最小值为( )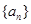 中,若
中,若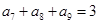 ,则该数列的前15项的和为 .
,则该数列的前15项的和为 .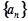 的前
的前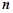 项的和为
项的和为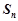 ,且
,且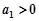 ,
,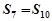 ,则使
,则使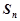 取到最大值的
取到最大值的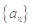 的前
的前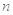 项和为
项和为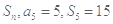 ,则数列
,则数列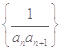 的前100项和为
的前100项和为