Question

4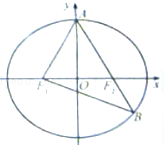．如图，椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左右焦点分别为F₁，F₂，A是椭圆C的一
个顶点，B是直线AF₁与椭圆C的另一个交点，∠F₁AB=90°，△F₁AB的面积为$\frac{4}{3}$
（1）求椭圆C的方程
（2）设P是椭圆C上的一个动点，点P关于原点的对称点为Q，求$\overrightarrow{BP}$•$\overrightarrow{BQ}$的取值
围．

Answer 1

分析 （1）设|BF₂|=t（t＞0），确定$t=\frac{a}{3}$，$|{AB}|=\frac{4a}{3}$，利用△F₁AB的面积为$\frac{4}{3}$，求出a，b，即可求椭圆C的方程；
（2）设动点P坐标为（x，y），确定B点坐标，利用向量的数量积公式，结合椭圆方程，即可求$\overrightarrow{BP}$•$\overrightarrow{BQ}$的取值
围．

解答 解：（1）$|{A{F_1}}|=\sqrt{{{|{AO}|}^2}+{{|{O{F_1}}|}^2}}=\sqrt{{b^2}+{c^2}}=a$，
又∵|AF₁|=|AF₂|，∴|AF₂|=a，----------------------------（1分）
设|BF₂|=t（t＞0），由椭圆定义知|BF₁|+|BF₂|=2a，∴|BF₁|=2a-t，-----------------（2分）
∵∠F₁AB=90°，∴${|{B{F_1}}|^2}={|{A{F_1}}|^2}+{|{AB}|^2}$，
即（2a-t）²=a²+（a+t）²，∴$t=\frac{a}{3}$，$|{AB}|=\frac{4a}{3}$----------------（3分）
∵${S_{△{F_1}AB}}=\frac{1}{2}|{A{F_1}}|•|{AB}|$，∴$\frac{4}{3}=\frac{1}{2}a•\frac{4}{3}a$，∴$a=\sqrt{2}$---------------（4分）
∵∠F₁AB=90°，|OA|=|OF₂|，∴b=c，
∵a²=b²+c²，∴b=1，---------------------------------（5分）
∴椭圆C的标准方程为$\frac{x^2}{2}+{y^2}=1$----------------------------------------（6分）
（2）设动点P坐标为（x，y），
∵点P关于原点的对称点为Q，∴Q点坐标为（-x，-y），-------------------------（7分）
由A（0，1），F₂（1，0），得直线AF₂的方程为y=1-x，-----------------------（8分）
联立$\left\{{\begin{array}{l}{y=1-x}\\{\frac{x^2}{2}+{y^2}=1}\end{array}}\right.$，得$\left\{{\begin{array}{l}{x=0}\\{y=1}\end{array}}\right.$或$\left\{{\begin{array}{l}{x=\frac{4}{3}}\\{y=-\frac{1}{3}}\end{array}}\right.$，∴B点坐标为$（\frac{4}{3}，-\frac{1}{3}）$，-----------------------（10分）
∴$\overrightarrow{BP}=（x-\frac{4}{3}，y+\frac{1}{3}）$，$\overrightarrow{BQ}=（-x-\frac{4}{3}，-y+\frac{1}{3}）$，
∴$\overrightarrow{BP}•\overrightarrow{BQ}=（x-\frac{4}{3}）（-x-\frac{4}{3}）+（y+\frac{1}{3}）（-y+\frac{1}{3}）=-{x^2}-{y^2}+\frac{17}{9}$------------------（11分）
=$-{x^2}-（1-\frac{x^2}{2}）+\frac{17}{9}=-\frac{1}{2}x{\;}^2+\frac{8}{9}$，------------------------------------------（12分）
点P在椭圆上，∴$-\sqrt{2}≤x≤\sqrt{2}$，∴0≤x²≤2，-------------------------------（13分）
∴$\overrightarrow{BP}•\overrightarrow{BQ}$的取值范围为$[-\frac{1}{9}，\frac{8}{9}]$．--------------------------------（14分）

点评 本题主要考查椭圆的定义与性质，直线、椭圆的位置关系，考查数形结合思想、化归与转化思想．