题目内容
6.已知平面α⊥平面β,且α∩β=l,在l上有两点A,B,线段AC?α,线段BD?β,并且AC⊥l,BD⊥l,AB=3,AC=6,BD=2,则CD的长为7.分析 连接BC,得△ACB为直角三角形,BC=5,由BD⊥l,得BD⊥BC.由此以求出CD.
解答 解:连接BC,∵AC⊥l,∴△ACB为直角三角形,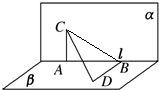
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}}$,
又∵BD⊥l,BD?β,α∩β=l,α⊥β,
∴BD⊥α,∴BD⊥BC.
在Rt△DBC中,CD=$\sqrt{B{D}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{6}^{2}+{2}^{2}}$=7.
故答案为:7
点评 本题考查线段长的求法,是基础题,解题时要认真审题,注意空想思维能力的培养.,属于中档题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
8.若将如图的展开图还原成成正方体,则∠ABC的度数为( )
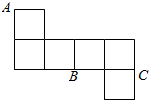

| A. | 120° | B. | 90° | C. | 60° | D. | 45° |