题目内容
双曲线 上的点
上的点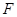 到一个焦点的距离为11,则它到另一个焦点的距离为( )
到一个焦点的距离为11,则它到另一个焦点的距离为( )
A.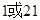 | B.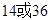 | C.2 | D.21 |
D
解析试题分析:设所曲线的左右焦点分别为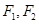 ,不妨设
,不妨设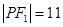 ,根据所曲线的定义知
,根据所曲线的定义知 所以
所以 或
或 ,而
,而 ,所以应该舍去,所以它到另一个焦点的距离为21.
,所以应该舍去,所以它到另一个焦点的距离为21.
考点:本小题主要考查所曲线定义的应用.
点评:圆锥曲线的定义十分重要,应用也十分广泛,应该给予充分的重视.另外本小题容易不舍1,要注意双曲线上的点到焦点的距离的最小值为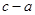 .
.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
抛物线 的焦点坐标为( )
的焦点坐标为( )
A. | B.(1,0) | C.(0,- ) ) | D.(- ,0) ,0) |
若抛物线 上一点
上一点 到
到 轴的距离为3,则点
轴的距离为3,则点 到抛物线的焦点
到抛物线的焦点 的距离为( )
的距离为( )
A. | B. | C. | D. |
“曲线 上的点的坐标都是方程
上的点的坐标都是方程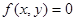 的解”是“曲线
的解”是“曲线 的方程是
的方程是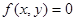 ”的( )条件
”的( )条件
| A.充要 | B.充分不必要 | C.必要不充分 | D.既不充分又不必要 |
已知椭圆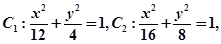 则
则
A. 与 与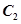 顶点相同. 顶点相同. | B. 与 与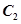 长轴长相同. 长轴长相同. |
C. 与 与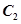 短轴长相同. 短轴长相同. | D. 与 与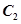 焦距相等. 焦距相等. |
双曲线两条渐近线互相垂直,那么它的离心率为 ( )
| A.2 | B.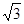 | C.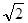 | D.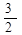 |
抛物线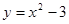 与直线
与直线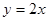 围成的封闭图形的面积是( )
围成的封闭图形的面积是( )
A.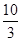 | B.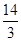 | C.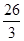 | D.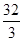 |
短轴长为 ,离心率
,离心率 的椭圆两焦点为
的椭圆两焦点为 , 过
, 过 作直线交椭圆于
作直线交椭圆于 两
两
点,则 的周长为( )
的周长为( )
A. | B. | C. | D. |
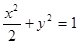 的右焦点作倾斜角为
的右焦点作倾斜角为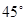 的直线
的直线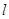 ,交椭圆于A、B两点,O为坐标原点,则
,交椭圆于A、B两点,O为坐标原点,则 ( )
( )
