题目内容
经过椭圆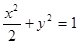 的右焦点作倾斜角为
的右焦点作倾斜角为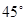 的直线
的直线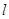 ,交椭圆于A、B两点,O为坐标原点,则
,交椭圆于A、B两点,O为坐标原点,则 ( )
( )
A. -3
B. 
C. -3或
D. 
B
解析试题分析:由椭圆方程为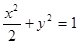 得a2=2,b2=1,c2=a2-b2=1,焦点为(±1,0).
得a2=2,b2=1,c2=a2-b2=1,焦点为(±1,0).
设直线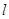 的方程为y=x-1.与椭圆方程联立
的方程为y=x-1.与椭圆方程联立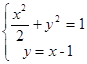 得:
得: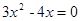 ,设A(x1,y1),B(x2,y2),则x1•x2=0,x1+x2=
,设A(x1,y1),B(x2,y2),则x1•x2=0,x1+x2=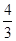 ,y1y2=(x1-1)(x2-1)=x1x2-(x1+x2)+1=1-
,y1y2=(x1-1)(x2-1)=x1x2-(x1+x2)+1=1-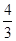 =
=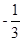 ,
,
所以 =x1x2+y1y2=
=x1x2+y1y2=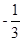 。故选B
。故选B
考点:本题考查直线与椭圆的综合应用;数量积;直线方程的点斜式。
点评:本题主要考查了椭圆的应用.当涉及过焦点的直线时,常需设出直线方程与椭圆方程联立利用韦达定理来解决.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
直线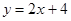 与抛物线
与抛物线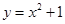 所围成封闭图形的面积是( )
所围成封闭图形的面积是( )
A.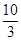 | B.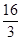 | C.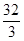 | D.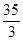 |
双曲线 上的点
上的点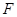 到一个焦点的距离为11,则它到另一个焦点的距离为( )
到一个焦点的距离为11,则它到另一个焦点的距离为( )
A.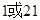 | B.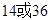 | C.2 | D.21 |
若方程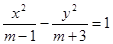 表示双曲线,则实数
表示双曲线,则实数 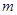 的取值范围是 ( )
的取值范围是 ( )
A. | B. |
C.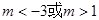 | D. |
中心在原点,焦点在y轴上,若长轴长为18,且两个焦点恰好将长轴三等分,则椭圆的方程是 ( )
A.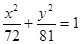 | B.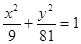 |
C.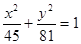 | D. |
椭圆 上的一点
上的一点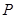 ,它到椭圆的一个焦点
,它到椭圆的一个焦点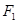 的距离是7,则它到另一个焦点
的距离是7,则它到另一个焦点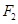 的距离是( )
的距离是( )
A.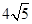 | B.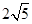 | C.12 | D.5 |
双曲线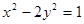 的右焦点的坐标为( )
的右焦点的坐标为( )
A.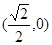 | B.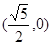 | C. | D.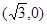 |
已知曲线C: 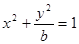 与抛物线
与抛物线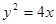 的一个交点为M,
的一个交点为M,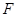 为抛物线的焦点,若
为抛物线的焦点,若 ,则b的值为
,则b的值为
A.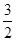 | B.-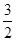 | C. | D.- |
抛物线  的准线方程是( ).
的准线方程是( ).
A.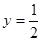 | B. | C.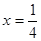 | D.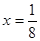 |