题目内容
抛物线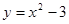 与直线
与直线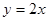 围成的封闭图形的面积是( )
围成的封闭图形的面积是( )
A.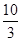 | B.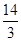 | C.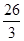 | D.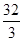 |
D
解析试题分析:由y=x2-3与y=2x,解得x=3,x=-1,当x=3,y=6;当x=-1,y=-2,
∴曲线y=x2-3及直线y=2x的交点为O(-1,-2)和A(3,6)因此,曲线y=x2-3及直线y=2x所围成的封闭图形的面积是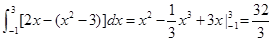 ,故答案为 D.
,故答案为 D.
考点:本题主要是考查曲线y=x2-3及直线y=2x,求它们围成的图形的面积,着重考查了定积分的几何意义和定积分计算公式等知识,属于基础题
点评:解决该试题的关键是联立方程组得到交点坐标,进而确定出积分上限和下限,然后根据定积分的几何意义得到结论。

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
已知椭圆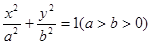 的左、右两焦点分别为
的左、右两焦点分别为 ,点
,点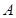 在椭圆上,
在椭圆上,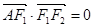 ,
,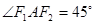 ,则椭圆的离心率
,则椭圆的离心率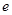 等于 ( )
等于 ( )
A. | B.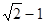 | C.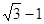 | D.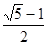 |
( )抛物线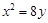 的准线方程是
的准线方程是
A.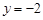 | B.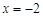 | C.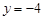 | D. |
双曲线 上的点
上的点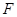 到一个焦点的距离为11,则它到另一个焦点的距离为( )
到一个焦点的距离为11,则它到另一个焦点的距离为( )
A.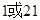 | B.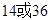 | C.2 | D.21 |
椭圆 的两焦点之间的距离为 ( )
的两焦点之间的距离为 ( )
A. | B. | C.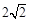 | D. |
若方程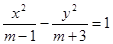 表示双曲线,则实数
表示双曲线,则实数 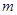 的取值范围是 ( )
的取值范围是 ( )
A. | B. |
C.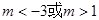 | D. |
中心在原点,焦点在y轴上,若长轴长为18,且两个焦点恰好将长轴三等分,则椭圆的方程是 ( )
A.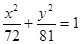 | B.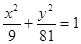 |
C.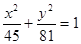 | D. |
双曲线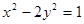 的右焦点的坐标为( )
的右焦点的坐标为( )
A.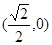 | B.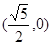 | C. | D.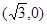 |
已知抛物线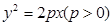 的焦点弦
的焦点弦 坐标分别为
坐标分别为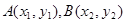 ,则
,则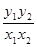 的值一定等于( )
的值一定等于( )
A.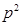 | B. | C. | D. |