题目内容
短轴长为 ,离心率
,离心率 的椭圆两焦点为
的椭圆两焦点为 , 过
, 过 作直线交椭圆于
作直线交椭圆于 两
两
点,则 的周长为( )
的周长为( )
A. | B. | C. | D. |
B
解析试题分析:由短轴长为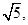 得
得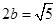 ;离心率
;离心率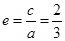 ,
,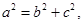 解得
解得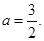
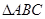 的周长为
的周长为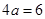 .
.
考点:椭圆的定义及性质.
点评:由椭圆的离心率及短轴长可求出a的值,然后利用椭圆的定义可知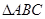 的周长为4a,从而求出
的周长为4a,从而求出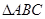 的周长.
的周长.

练习册系列答案
相关题目
双曲线 上的点
上的点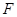 到一个焦点的距离为11,则它到另一个焦点的距离为( )
到一个焦点的距离为11,则它到另一个焦点的距离为( )
A.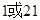 | B.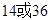 | C.2 | D.21 |
双曲线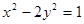 的右焦点的坐标为( )
的右焦点的坐标为( )
A.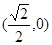 | B.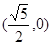 | C. | D.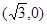 |
已知曲线C: 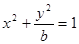 与抛物线
与抛物线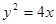 的一个交点为M,
的一个交点为M,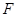 为抛物线的焦点,若
为抛物线的焦点,若 ,则b的值为
,则b的值为
A.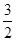 | B.-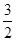 | C. | D.- |
若焦点在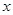 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为 ,则
,则 ( )
( )
A. | B. | C. | D. |
抛物线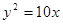 的焦点到准线的距离是
的焦点到准线的距离是
A.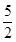 | B.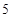 | C.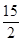 | D.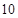 |
已知抛物线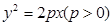 的焦点弦
的焦点弦 坐标分别为
坐标分别为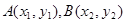 ,则
,则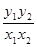 的值一定等于( )
的值一定等于( )
A.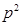 | B. | C. | D. |
抛物线  的准线方程是( ).
的准线方程是( ).
A.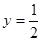 | B. | C.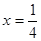 | D.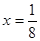 |
已知双曲线方程为 ,过
,过 的直线
的直线 与双曲线只有一个公共点,则
与双曲线只有一个公共点,则 的条数共有( )
的条数共有( )
| A.4条 | B.3条 | C.2条 | D.1条 |